DVS 1608

Version: September 2011 Edition

List of Classification Parameters

Evaluation Distance

Reference distance to find the evaluation location from the weld element at which the stress values are extracted.

Weld Width

Width of the weld material from the web wall. This parameter is ignored if specifying the evaluation distance is done manually.

Note: Refer to - Find Evaluation Positions.

Grinding Bonus

Parameter to specify if the grinding bonus has to be considered or not.

Effective Weld Thickness

This parameter is used to consider the influence of welds which do not cover the same cross section area as indicated by the shell element in the respective evaluation location. It modifies the stress at the evaluation location based on the ratio to the shell thickness. (a > 0)

A r = T_{i} \cdot T_{f}

$T i$ : Thickness influence represents the resultant maximum weld thickness. It varies based on the weld type. this parameter is location specific.
$T f$ : Indicates which shell thickness you need for the calculation of effective weld thickness ( a ). Valid options are t and t_min, also location specific. t = thickness of welded shell. t_min = min thickness of all connected shells.

Note: Refer to - Common Classification Parameters

Mean Stress Sensitivity – Normal

Mean stress sensitivity factor used for the normal direction evaluation.

Mean Stress Sensitivity – Shear

Mean stress sensitivity factor used for the shear direction evaluation.

Notch Class - Transverse Location_X

Notch class definition considered for the fatigue limit calculation for the normal stress component in the transverse direction (perpendicular to the axis of the weld) at ‘X’.

Notch Class - Longitudinal Location_X:

Notch class definition considered for the fatigue limit calculation for the normal stress component in the longitudinal direction (parallel to the axis of the weld) at ‘X’.

Notch Class - Shear Location_X

Notch class definition considered for the shear stress component at ‘X’.

Note: Where ‘X’ can be any evaluation location.

Material Yield - Location_X

Material yield value used for the static evaluation.

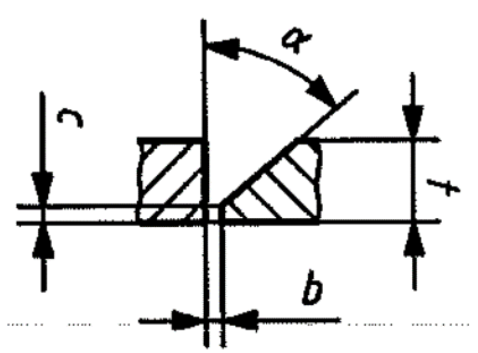
Groove Gap (b)

Gap between the two plates at the location of weld. b in Figure 1.

Groove Depth (h)

Height of the groove from the top, calculated as t - c from Figure 1.

Groove Angle (alpha - deg)

Angle of the groove/plate walls at the location of weld. a in Figure 1.

Note: Refer to Figure 1 for the groove parameters. These groove parameters have been derived from the En 15085 standard. Refer to Common Classification Parameters.

Formulation

Stress Component considered for evaluation

σ_T: Transverse component perpendicular to the axis of the weld
σ_L: Longitudinal component parallel to the axis of the weld
τ: Shear Component

Corrected stress calculation

The stress value correction is carried out using the effective weld thickness.

Note: Refer to - Common Classification Parameters

Calculation of the Assessment stress value (numerator in utilization formulae)

σ_TA (Stress Amplitude) = (σ_Tmax -
                                σ_Tmin) / 2

The stress amplitude is used as the numerator for the utilization calculation.

Fatigue Limit Calculation

The fatigue limit values (σ_Tzul, σ_Lzul, and τ_zul), are calculated based on the following regimes of Stress Ratio ®,

Reference: the DVS1608 regulation document section 7.2.2.

For nominal stress (longitudinal σ_Lzul and transverse σ_Tzul)

Regime 1:

(R_{σ} > 1)

σ_{z u l} = 54 \cdot {1.04}^{- x} (M P a)

Regime 2:

(- \infty \leq R_{σ} \leq 0)

σ_{z u l} = 46 \cdot {1.04}^{- x} (\frac{1}{1 + M_{σ} \frac{1 + R_{σ}}{1 - R_{σ}}}) (M P a)

Regime 3:

(0 < R_{σ} < 0.5)

σ_{z u l} = 42 \cdot {1.04}^{- x} (\frac{1}{1 + \frac{M_{σ}}{3} (\frac{1 + R_{σ}}{1 - R_{σ}})}) (M P a)

Regime 4:

(0.5 \leq R_{σ} < 1)

σ_{z u l} = 36.5 \cdot {1.04}^{- x} (M P a)

$M_{τ}$ is the mean stress sensitivity, the exponent x in the above equations is queried from the below notch detail tables:

Curve	B	B-	B+	C	C-	C+	D	D-
x	6	7	8	9	10	11	12	13

Curve	E1+	E1	E1-	E4+	E4	E4-	E5+	E5	E5-	E6+	E6	E6-
X	14	15	16	17	18	19	20	21	22	23	24	25

Curve	F1+	F1	F2
x	26	27	28

For shear stress, $τ_{z u l}$ ,

Regime 2:

(- 1 \leq R_{τ} \leq 0)

τ_{z u l} = 28 \cdot {1.04}^{- x} (\frac{1}{1 + M_{τ} \frac{1 + R_{τ}}{1 - R_{τ}}}) (M P a)

Regime 3:

(0 < R_{τ} < 0.5)

τ_{z u l} = 26.5 \cdot {1.04}^{- x} (\frac{1}{1 + \frac{M_{τ}}{3} (\frac{1 + R_{τ}}{1 - R_{τ}})}) (M P a)

Regime 4:

(R_{τ} \geq 0.5)

τ_{z u l} = 24.4 \cdot {1.04}^{- x} (M P a)

$M_{τ}$ is the mean stress sensitivity, the exponent x in the above equations is queried from the below notch detail table:

Curve	G	H
x	0	9

The grinding bonus and the thickness factor is applied to the calculated fatigue limit for longitudinal and transverse and just the thickness factor to the calculated shear fatigue limit.

Utilization Factor Calculation

U_T = σ_TA /
                                    σ_Tzul

U_L = σ_LA / σ_Lzul

U_τ = τ_A / τ_zul

Resultant Utilization Calculation

U_{R} = \sqrt[2]{{(U_{T})}^{2} + {(U_{L})}^{2} + {(U_{τ})}^{2} + (U_{T} X U_{L})}