Advanced Averaging

Advanced averaging means that tensor (or vector) results are transformed into a consistent system and then each component is averaged separately to obtain an average tensor (or vector).

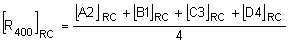
The invariants are calculated from this averaged tensor. The consistent system can be the global or the user-defined system for solid elements. For shell elements, the consistent system is the nodal projection system, which is the projected global or user-defined system on the nodal projection plane (described in the Projection rule).

In the example shown in the Nodal Averaging of Elemental Results topic, the averaged tensor at node 400 is:

Where, 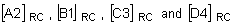are tensors transformed to the reference system for corners A2, B1, C3, and D4, respectively.

The components are extracted and the invariants are computed from this averaged tensor or vector .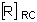

The averaging methods for solid elements and shell elements are different.

Element Type	Reference System	Projection Rule	Description
Solid	Global	N/A	All corresponding tensors and vectors are transformed to the global coordinate system and an average tensor/vector is calculated. The components and invariants are obtained from this tensor/vector as explained above.
	User-defined	N/A	Variation ON All corresponding tensors and vectors are transformed to the user-defined coordinate system and an average tensor/vector is calculated. The components and invariants are obtained from this tensor/vector. Variation OFF All corresponding tensors and vectors are transformed to the global coordinate system and an average tensor/vector is calculated. Then, this average tensor/vector is transformed to the user-defined system for components extraction and invariants calculation.
Shell	Global	ON	The global co-ordinate system is projected to the Nodal Projection plane (described in the Projection rule) to obtain the Nodal Projection system. All corresponding tensors/vectors are then transformed to the Nodal projection system and an average tensor/vector is calculated. The components and invariants are obtained from this tensor/vector. As a result, even if the reference system is the same, the projected systems in participating elements can be different. Simple averaging for components ignores variations in systems.
		OFF	All corresponding tensors and vectors are transformed to the global coordinate system and an average tensor/vector is calculated. The components and invariants are obtained from this tensor/vector.
	User-defined	ON	The user-defined co-ordinate system is projected to the Nodal Projection plane (described in the Projection rule) to obtain the Nodal Projection system. Variation ON All corresponding tensors/vectors are then transformed to the Nodal projection system and an average tensor/vector is calculated. The components and invariants are obtained from this tensor/vector. Variation OFF All corresponding tensors and vectors are transformed to the global coordinate system and an average tensor/vector is calculated. Then, this average tensor/vector is transformed to the Nodal projection system for components extraction and invariants calculation.
		OFF	Variation ON All corresponding tensors and vectors are transformed to the user-defined coordinate system and an average tensor/vector is calculated. The components and invariants are obtained from this tensor/vector. Variation OFF All corresponding tensors and vectors are transformed to the global coordinate system and an average tensor/vector is calculated. Then, this average tensor/vector is transformed to the user-defined system for components extraction and invariants calculation.

Valid reference coordinate system: Global and User-defined.