MV-7013: Inverted Pendulum Control Using MotionSolve with Compose Subroutines

In this tutorial, you will learn how to use MotionView, MotionSolve, and Compose to design a control system that stabilizes an inverted pendulum.

The goal of this tutorial is to design a regulator using the pole placement method. The inverted pendulum MDL model file is supplied.

The tutorial steps include:
  • Check the stability of the open loop system.
  • Export linearized system matrices A, B, C, and D using MotionSolve linear analysis.
  • Design a controller using Compose.
  • Implement a controller in MotionView.
  • Check the stability of a closed loop system using MotionSolve linear analysis.
  • Add disturbance forces to the model and run simulation using MotionSolve.

The image below shows the classic inverted pendulum on a slider. The system has two degrees of freedom leading to four state variables. The vertically upright position of the pendulum is unstable. The goal is to design a regulator to stabilize this configuration.



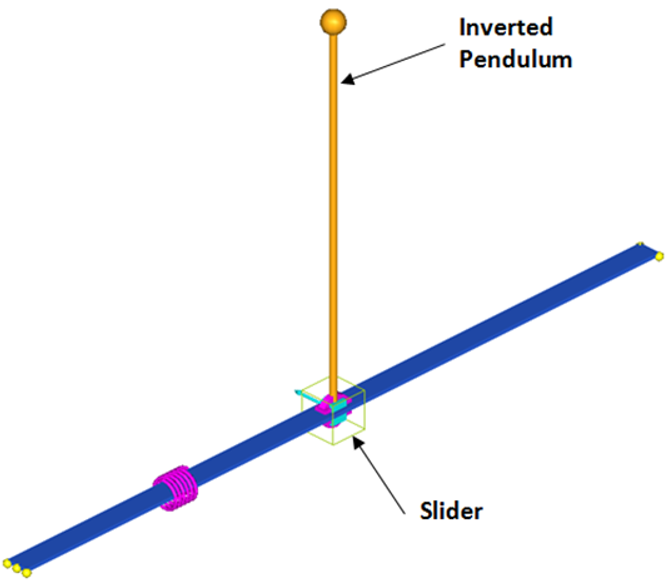
Figure 1. Inverted Pendulum Model

To achieve the goal, find a full-state feedback control law. The control input is a force applied to the slider along the global X-axis. Plant output is the pendulum angle of rotation about the global Y-axis.

Start by loading the file inv_pendu.mdl, located in [installation_directory]\tutorials\hwdesktop\mv_hv_hg\mbd_modeling\motionsolve, into MotionView and save it to your working directory. Upon examination of the model topology, notice that everything needed for this exercise is included in the model. However, depending on which task you are performing, it may be necessary to activate or deactivate certain entities.

References: Feedback Control of Dynamic Systems, G. G. Franklin, J. D. Powell, and A. Emami-Naeini, Third Edition, Addison Wesley.

Determine the Stability of the Open Loop Model

Compute the eigenvalues to determine the stability of the inverted pendulum.

  1. From the Project Browser, click Forces.Verify that Control Force - OL is activated, while Control Force - CL and Disturbance-step are deactivated.
  2. From General Actions toolbar, click Run, .
  3. From the Simulation type drop-down menu, select Static+Linear.
  4. Specify the output filename as inv_pendu_ol_eig.xml.
  5. Select the MDL animation file (.maf) option.
  6. Click Run.
  7. Once the solution is complete, close the solver execution window and the Message Log.
    The eigenvalues computed by MotionSolve are shown in the table below and can be viewed in the inv_pendu_ol_eig.eig file using a text editor.
    NUMBER NATURAL_FREQ(HZ) DAMPING_RATIO REAL(HZ) IMAG_FREQ(HZ)
    1 1.624738E-02 1.000000E+00 -1.624738E-02 0.000000E+00
    2 4.003669E-01 1.000000E+00 -4.003669E-01 0.000000E+00
    3 0.000000E+00 1.000000E+00 5.582830E-01 0.000000E+00
    4 1.733217E+00 1.000000E+00 -1.733217E+00 0.000000E+00

    There is one eigenvalue with a positive real part, indicating that the system is unstable in the current configuration.

  8. Click Animate.
    The result animation H3D file is loaded in the adjacent window.
  9. From the Results Browser, select individual modes.


    Figure 2.
  10. Click Start/Pause Animation, , to visualize the mode shape.

Obtain a Linearized Model

Usually, the first step in a control system design is to obtain a linearized model of the system in the state space form:

ẋ = Ax+Bu

y = Cx+Du

where A, B, C, and D are the state matrices, x is the state vector, u is the input vector, and y is the output vector. The A, B, C, and D matrices depend on the states chosen (by the solver), inputs, and outputs. You only need to define the inputs and outputs.

  1. Return to the MotionView window.
  2. From the Project Browser, expand the Solver Variables folder and examine the entities.
    • Control Force Variable - OL is used to define the control plant input, which is a force named Control Force - OL. This force is applied to the slider body. This variable is set to zero. It is needed by MotionSolve to properly generate the linearized system matrices.
    • The solver variable Pendulum Rotation Angle defines the control plant output and measures the pendulum rotation about the Global Y-axis.
  3. From the Project Browser, expand the Solver Array folder and examine the solver arrays that are defined.
    1. Select Plant-I. This array defines a solver array entity of type Plant-Input.
    2. Ensure that Solver Variable is set to Control Force Variable - OL.
    3. Ensure that Use in linearization check box is ticked.
    4. Select Plant-O. This array defines a solver array entity of type Plant-Output.
    5. Ensure that Solver Variable is set to Pendulum Rotation Angle.
    6. Ensure that Use in linearization check box is ticked.
  4. Click Run, .
  5. From the Simulation type drop-down menu, select Linear.
  6. Specify the output filename as inv_pendu_state_matrices.xml.


    Figure 3. Linear Tab in the Simulation Settings Dialog for Specifying the Compose Matrix Files Output
  7. From the Simulation Settings dialog > Linear tab > General State-Space Matrix, select Altair Compose/Activate OML.
  8. From the Main tab, click Run.
    A new file is created with the base name inv_pendu_state_matrices.oml.
    The states chosen by the MotionSolve solver are:
    • Angular displacement about the global-Y axis.
    • Translation displacement along the global X-axis.
    • Angular velocity about the global-Y axis.
    • Translation velocity along the global X-axis of the pendulum body center of mass marker.
    Note: MotionSolve writes the selected states into the log file if Write debug info is selected under Output Options.


    Figure 4. General Tab in Output Options Dialog for Specifying the Write debug info.

Design a Control System in Compose

A detailed discussion of control system design is beyond the scope of this tutorial. However, the steps to design a regulator using pole placement[1] to stabilize the inverted pendulum are described briefly. For details, refer to the standard controls text and the Compose documentation.

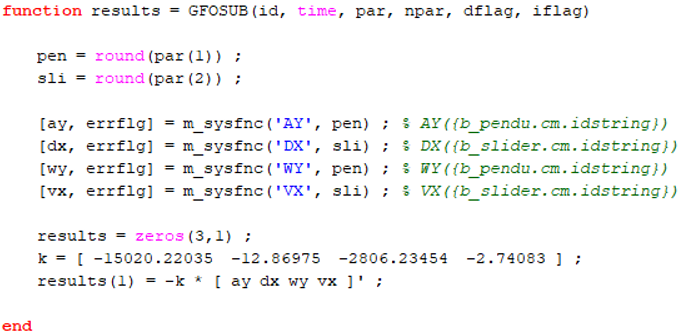
Use Compose to verify that the system is completely state controllable[1, 2].
  1. Employ a full-state feedback control law u = − k ∗ x, where u is the control input, k is the gain vector, and x is the state vector.
  2. Assuming the necessary pole locations are stored in vector P, use the pole placement method to compute k.
  3. Load the state space matrices into the Compose workspace by loading/running the script inv_pendu_state_matrices.oml.
  4. For poles P at 3 Hz, type the following into the command window:
    p = 2*pi*3 * [ -1 -1 -1 -1 ] ; k = acker( A , B , p )
  5. The Compose acker function yields to the following processing and result:
    k = [Matrix] 1 x 4
-15020.22034 -12.86975 -2806.23453 -2.74083

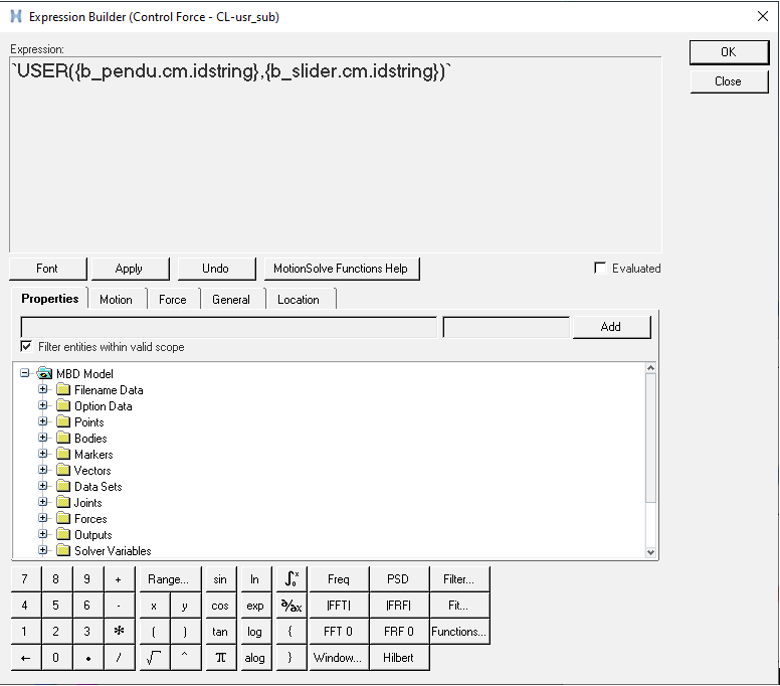
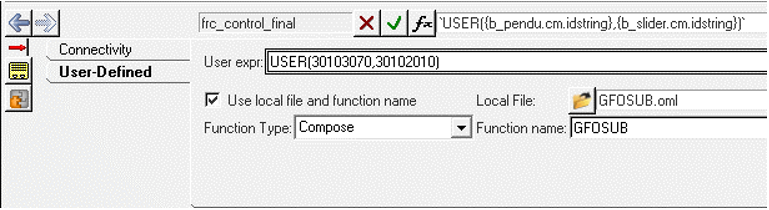
Implement the Control Force in MotionView

The control force is u = − k ∗ x. The model contains a solver variable called Control Force Variable - CL. Replace the Force Entity with a user-defined Compose script using GFOSUB. GFOSUB accesses the states of the system via m_sysfnc.

Write the Compose Script

  1. Create a new OML file in Compose.
  2. Enter the following to define the function GFOSUB:
    function results = GFOSUB(id, time, par, npar, dflag, iflag)
    For more details on this subroutine, please see GFOSUB.
    par contains the IDs of the CM markers for the pendulum and the slider. IDs are defined later in via MotionView. For the sake of robustness, verify that the ID is an integer.
  3. On a new line, enter:
    pen = round(par(1)) ; sli = round(par(2)) ;
  4. Use m_sysfnc to save it as a variable. Enter the following: 
    [ay, errflg] = m_sysfnc('AY', pen);
[dx, errflg] = m_sysfnc('DX', sli);
[wy, errflg] = m_sysfnc('WY', pen); 
[vx, errflg] = m_sysfnc('VX', sli);
  5. Write the control force for the inverse pendulum. It is the dot product between the gain vector (k) and the state vector (x) elements. Apply a GFOSUB on one body (Force_Vector_OneBody), and for that, the returned array needs to be of dimension 3. 
    results = zeros(3,1) ;
k = [ -15020.22035 -12.86975 -2806.23454 -2.74083 ] ;
results(1) = -k * [ ay dx wy vx ]' ;
  6. Close the function with an end command.
    Below is an example of the complete function, with your script resembling the following example:


    Figure 5.
  7. Save this file to your <working directory> as GFOSUB.oml.

Implement the Compose Script

  1. From the Project Browser, click Forces. Deactivate Control Force – OL and activate Control Force – CL.
  2. From the Connectivity tab, select User-defined properties.
  3. From the User-Defined tab, edit the Force value with the Expression Builder to include the pendulum and slider marker idstring.


    Figure 6.
  4. Click OK.
  5. Select Use local file and function name, and select Compose from the Function Type drop-down menu.
  6. Use to select GFOSUB.oml from your <working directory>.
  7. Verify Function name is set to GFOSUB.


    Figure 7.

Check the Stability of a Closed Loop System

  1. From the Run panel > Simulation type drop-down menu, select Linear.
  2. Specify the output file as inv_pendu_cl_eig.xml and click Run, .
    The eigenvalues are shown below.
    NUMBER NATURAL_FREQ(HZ) DAMPING_RATIO REAL(HZ) IMAG_FREQ(HZ)
    1 2.681249E+00 1.000000E+00 -2.681249E+00 0.000000E+00
    2 3.380362E+00 1.000000E+00 -3.380362E+00 0.000000E+00
    3 2.989457E+00 9.933140E-01 -2.969470E+00 3.451144E-01
    4 2.989457E+00 9.933140E-01 -2.969470E+00 -3.451144E-01

    They all have negative real parts, hence the system is stabilized. Note that the negative real parts are close to the necessary poles ( 3 Hz ).

Add Disturbance Force and Run a Transient Simulation

  1. From the Project Browser, click Forces and activate Disturbance-step.
    This force creates a small disturbance to the pendulum during a transient analysis. The purpose of the controller is to correct the disturbance such that the inverted pendulum does not fall over. The disturbance is defined as a step function:
    1. Fx=`step(TIME,.1,0,.5,50) + step(TIME,1,0,1.5,-50)`
    2. Fy=0
    3. Fz=0
  2. From the Project Browser, click Outputs and activate Output control force - final and Output Disturbance step.
  3. From the toolbar, click Run, .
  4. From the Simulation type drop-down menu, select Transient.
  5. Specify the output filename as inv_pendu_dyn.xml.
  6. Specify the End time and Print interval as 3.0 and 0.01, respectively.
  7. From the Main tab, click Run.
  8. Once the job is completed, close the solver window and plot the following results in a new HyperGraph page using inv_pendu_dyn.mrf.
    Output Y-Type Y-Request Y-Component
    control force Marker Force REQ/70000014 Control Force - CL on Body slider(Output control force - final) FX
    disturbance force Marker Force REQ/70000017 Disturbance-step on Body slider(Output Disturbance step) FX
    slider displacement -X Marker Displacement REQ/70000006 Body slider(Output slider-disp) DX
    pendulum angular displacement Expressions REQ/70000016 Output Pendu rotation F2
  9. The plots of disturbance force, control force, slider x displacement, and pendulum angular displacement are shown below.


    Figure 8. Plots of Disturbance and Control Forces as well as Slider Translational and Pendulum Angular Displacements