MV-3010: Optimization using MotionView - HyperStudy
- Perform an optimization study in the MotionView-HyperStudy environment
- Compare the baseline and optimized models
Theory
- The design constraints
- The objective function
- The design variables
Design variables change during optimization. The design variables always have a certain range within which they can be modified. Typical examples of design variables are thickness of shell elements, shape vectors, and masses.
The changes in the design variables cause some change in model responses. Such responses can become either objective function or design constraints. Examples of such responses include displacements and forces.
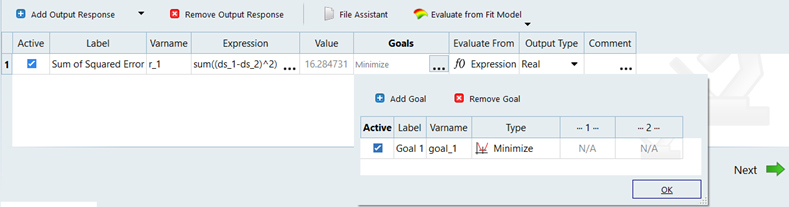
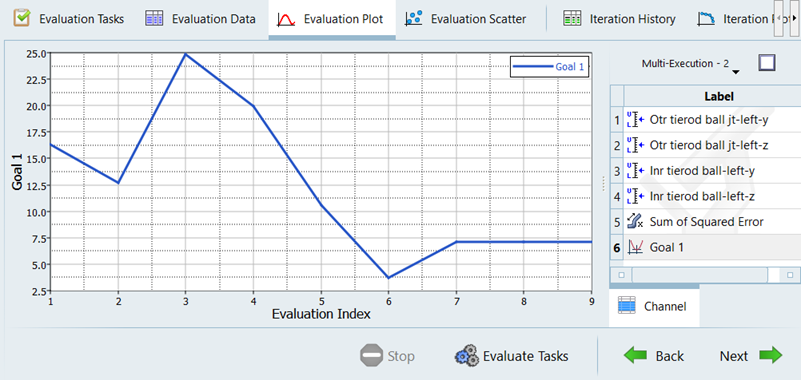
The response to be minimized or maximized becomes the objective function, while the rest of the responses that need to be within a certain tolerance range become constraints. Only one response can be defined as objective function.
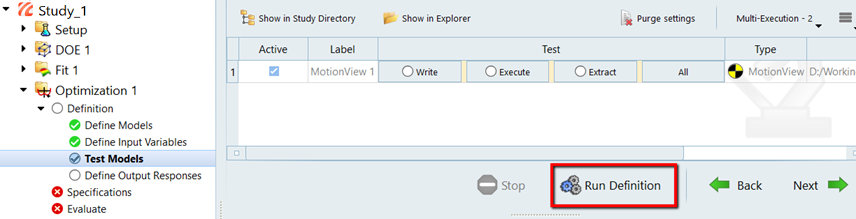
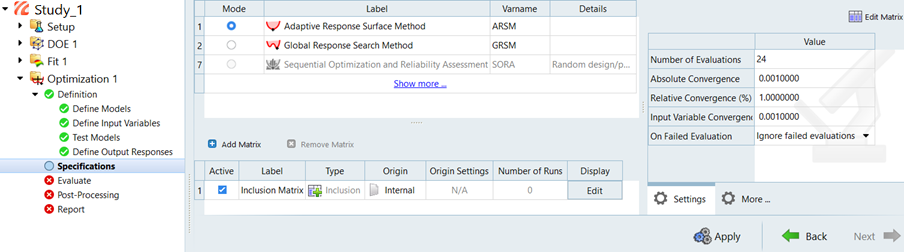
HyperStudy can be used to set-up and perform an optimization study on a MotionView model. You can also use HyperStudy to perform optimization studies involving both linear and non-linear CAE analysis as well as perform optimization of mathematical equations using Templex. HyperStudy creates the input parameter files using Templex and provides iterative changes to them during the optimization process. HyperStudy uses HyperOpt (a general purpose, wrap around software) as the optimization engine to perform optimization, in conjunction with both linear and non-linear CAE analysis software. HyperOpt uses a robust sequential response surface methodology for optimization.
The files needed for this tutorial are hs.mdl, target_toe.csv (used in tutorial MV-3000); Setup.hstudy saved in tutorial MV-3000 and the setup_1-def folder created in tutorial MV-3000.
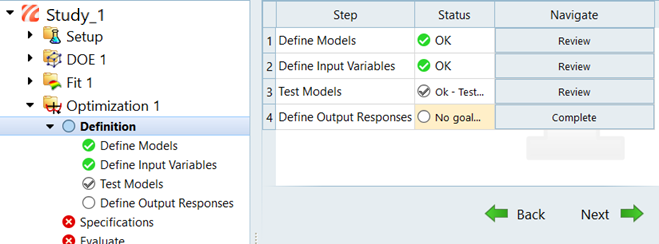
In the following steps you will perform an optimization study on a front SLA suspension model and determine the optimum coordinate positions of the inner and outer tie-rod points while trying to achieve a target toe curve. The baseline model will then be compared with the optimized model.