ACU-T: 5201 Coupled Simulation of a Check Valve using AcuSolve and MotionSolve
Prerequisites
This tutorial introduces you to the workflow for setting up an AcuSolve-MotionSolve co-simulation using HyperMesh Desktop. Prior to starting this tutorial, you should have already run through the introductory HyperWorks tutorial, ACU-T: 1000 HyperWorks UI Introduction, and have a basic understanding of HyperMesh, AcuSolve, and HyperView. To run this simulation, you will need access to a licensed version of HyperMesh and AcuSolve.
Since the HyperMesh database (.hm file) contains meshed geometry, this tutorial does not include steps related to geometry import and mesh generation.
Problem Description

Figure 1. Schematic of Check Valve with Spring-Loaded Shutter
The pipe has an inlet diameter of 0.08 m and is 0.4 m long. The check-valve assembly is 0.085 m downstream of the inlet. It consists of a plate 0.005 m thick with a centered orifice 0.044 m in diameter and a shutter with an initial position 0.005 m from the opening, simulating a nearly closed condition. The shutter plate is 0.05 m in diameter and 0.005 m thick. The shutter plate is attached to a stem 0.03 m long and 0.01 m in diameter. The mass of the shutter and stem is 0.2 kg and its motion is affected by a virtual spring with a stiffness of 2162 N/m. The motion of the valve shutter is limited by a stop mounted on a perforated plate downstream of the shutter.
Modeling the geometry as a 30° section requires that the fluid model is set up to be consistent with the rigid-body model. Since only 1/12 of the rigid body is modeled, the forces computed by AcuSolve that act on the valve shutter represent 1/12 of the actual force on the device. The rigid-body-dynamics model was set up in MotionSolve with scaled settings of mass and spring stiffness to account for the fact that you are only modeling a small section of the full geometry. Additional information regarding the setup of this problem in MotionSolve is provided in the MotionSolve documentation.
The fluid in this problem is water, which has a density (ρ) of 1000 kg/m3 and a molecular viscosity (μ) of 1 X 10-3.
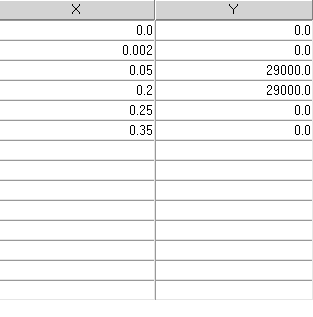
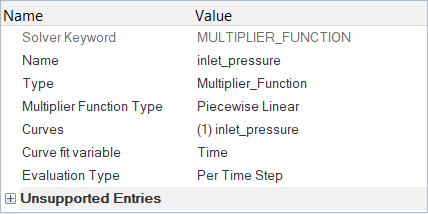
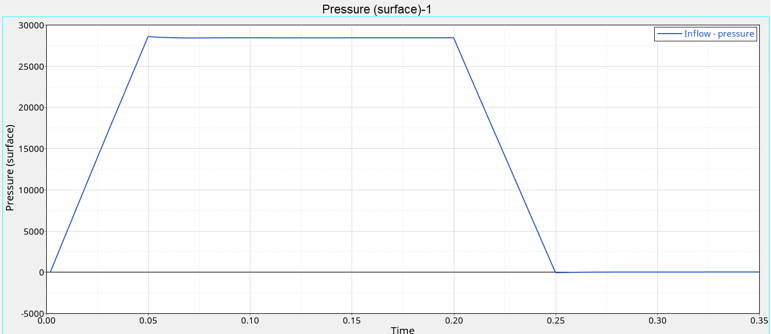
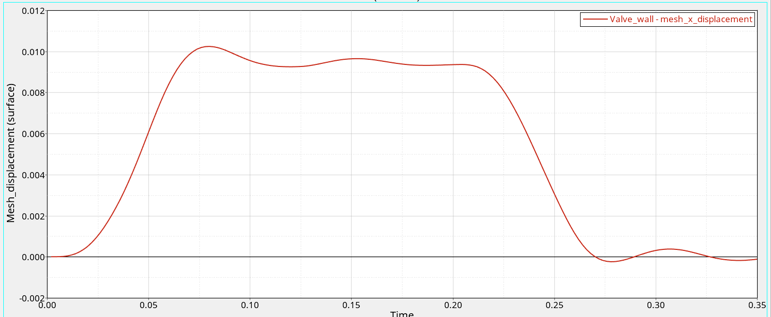
At the start of the simulation the flow field is stationary. Flow is driven by the pressure at the inlet, which varies over time as a piecewise linear function shown in Figure 2. As the pressure at the inlet rises, the flow will accelerate as the valve opens. The turbulence viscosity ratio is assumed to be 10.
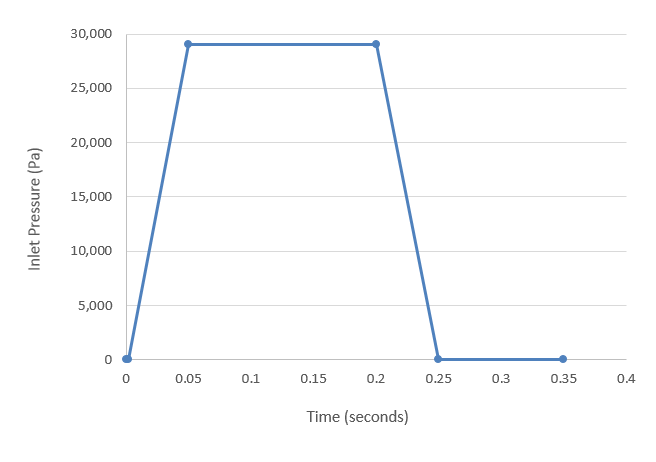
Figure 2. Transient pressure at the inlet
Prior simulations of this geometry indicate that the average velocity at the inlet reaches a maximum of 0.98 m/s. At this velocity, the Reynolds number for the flow is 78,400. When the Reynolds number is above 4,000 it is generally accepted that flow should be modeled as turbulent. Mesh motion will be modeled using arbitrary mesh movement (arbitrary Lagrangian-Eulerian mesh motion).
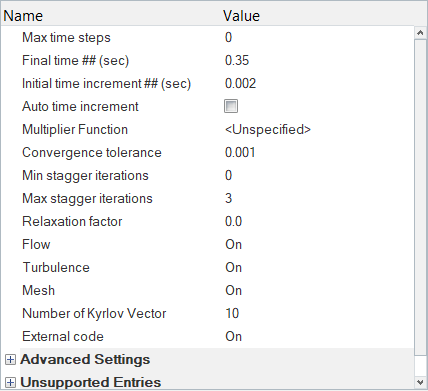
For this case, the transient behavior of interest occurs in the time it takes for the pressure to ramp up and ramp back down, which is given by the transient pressure profile. To allow time for the spring to recover additional time will be simulated. For this tutorial 0.1 s is added after the pressure drops back to initial conditions for a total duration of 0.35 s.
Another critical decision in a transient simulation is choosing the time increment. The time increment is the change in time during a given time step of the simulation. It is important to choose a time increment that is short enough to capture the changes in flow properties of interest, but does not require unnecessary computation time. The change in inlet pressure from initial conditions to maximum occurs over 0.048 s. A time increment of 0.002 s would allow for excellent resolution of the transient changes without requiring excessive computational time.
Open the HyperMesh Model Database
Set the General Simulation Parameters
Set the Analysis Parameters
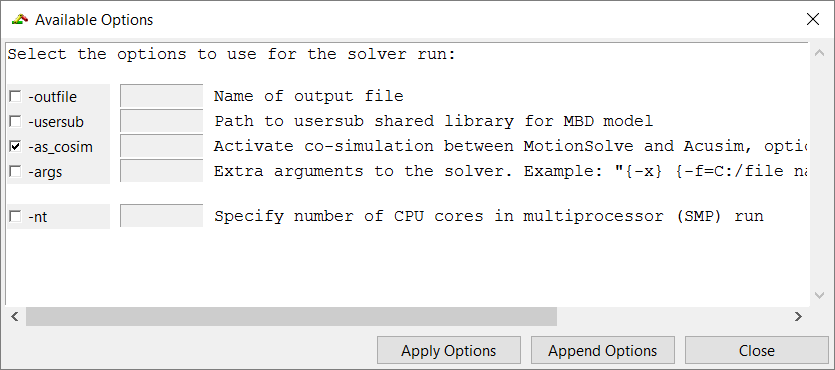
Specify the Solver Settings
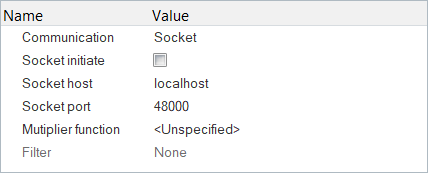
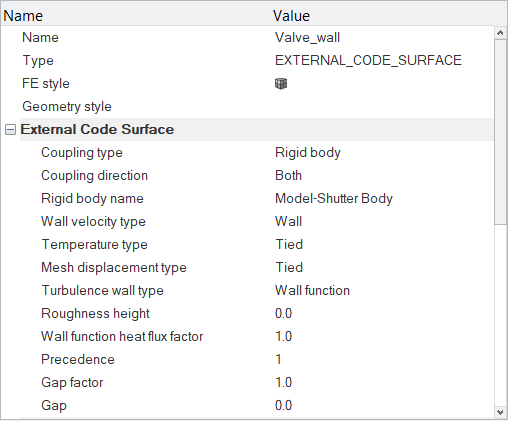
Set External Code Parameters for Communication with MotionSolve
Define the Nodal Output Frequency
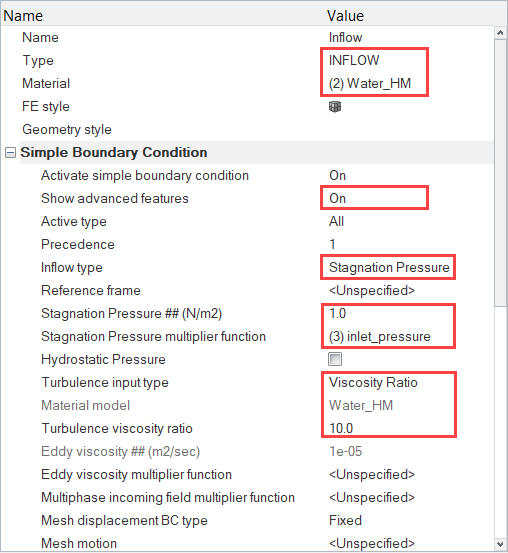
Set the Boundary Conditions
Create a Multiplier Function for Inlet Pressure
Set the Boundary Conditions
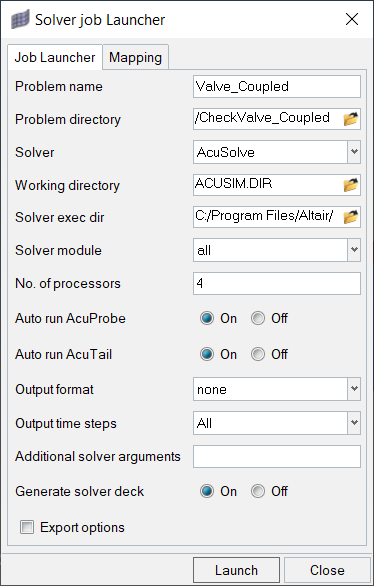
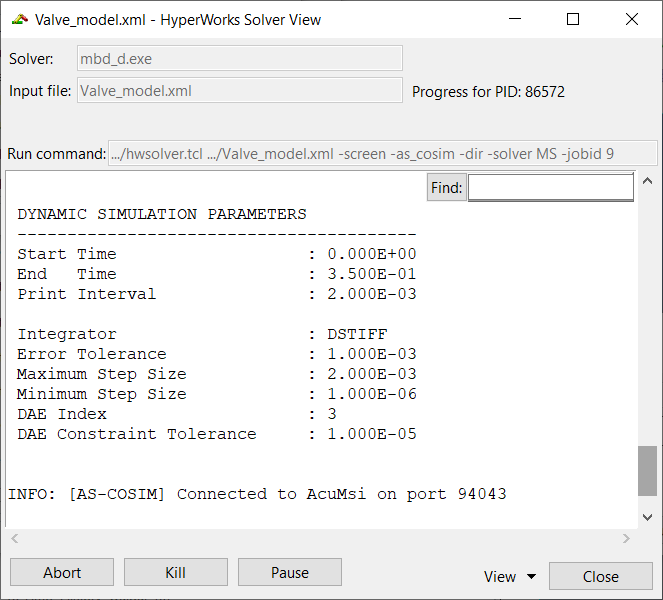
Compute the Solution
- Start AcuSolve
- Start MotionSolve
The next sets of steps provide instructions for these two tasks.
Run AcuSolve
In this step, you will launch AcuSolve to compute a solution for this case.
Run MotionSolve
Monitor the Solution with HyperGraph
Post-Process the Results with HyperView
In this step, you will create an animation of the valve motion as the water flows across the valve. Once the solver run is complete, close the AcuProbe and AcuTail windows. In the HyperMesh Desktop window, close the AcuSolve Control tab and save the model.
Switch to the HyperView Interface and Load the AcuSolve Model and Results
Create an Animation of Velocity Magnitude
Display Pressure and Velocity Contours on a Section Cut
Summary
In this tutorial, you learned the basic workflow to set up a co-simulation using AcuSolve and MotionSolve. The tutorial introduced you to the steps involved in setting up external code communication between AcuSolve and MotionSolve using HyperMesh Desktop and then running the simulation and post-processing the results using HyperView. You also learned how to create a vector plot on an existing contour plot on a cut plane.

 on the Standard Views toolbar.
on the Standard Views toolbar.