Power Law Model |

|

|

|

|
|
Power Law Model |

|

|

|

|
This is a two parameter model and it is described by the following equation.

This model describes the viscosity using a power-law relationship. The exponent n determines the nature of the relationship.
n < 1 Shear thinning or Pseudoplastic
n > 1 Shear thickening or dilalatant
n = 1 Newtonian
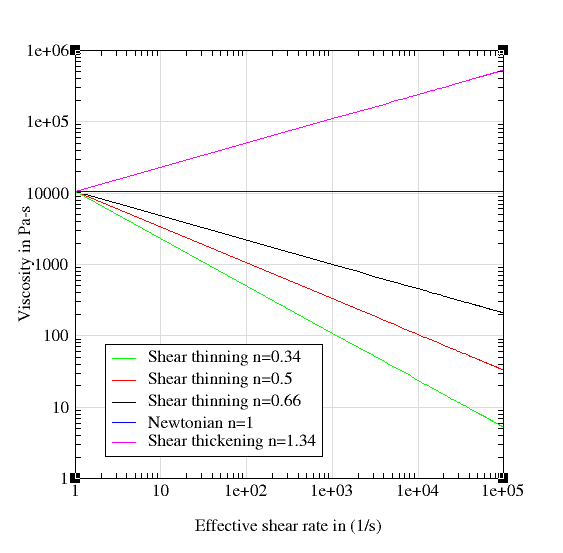
For most polymers, Exponent n is less than 1. When the exponent is less than 1, viscosity of the polymer decreases with increase in the shear rate. This behavior is called shear thinning. On the other hand, when the exponent is greater than 1, viscosity increases with shear rate and this behavior is called shear thickening. The following figure shows viscosity as a function of exponent (consistency = 1.05e+04)
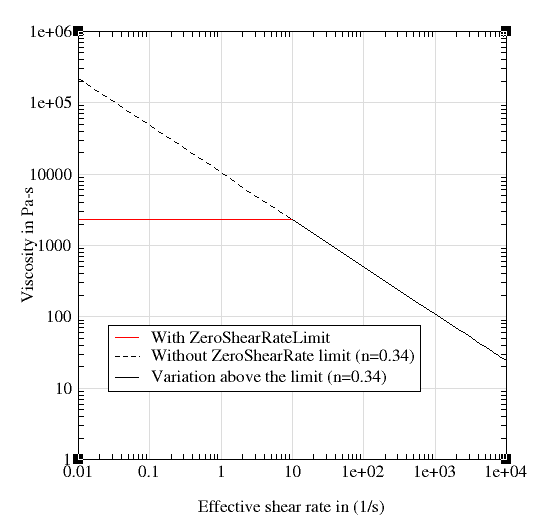
One of the disadvantages of the power-law model is, as the shear rate tends to zero (when the exponent is less than 1) the viscosity tends to infinity. This setback is overcome in HyperXtrude by defining a ZeroShearRateLimit. Typically, this value is chosen based on the experimental data used to determine the model coefficients. For instance, if the ZeroShearRateLimit is set to 10.0, then HyperXtrude will use this value to compute the viscosity whenever the effective shear rate of the flow field is less than the ZeroShearRateLimit. The following figure shows this effect for a power-law model with consistency 1.05e+04 and exponent 0.34.
In addition to this, a few additional parameters arise due the temperature dependence of material data; these variables are discussed in Temperature Dependence.
Syntax
Syntax of the data packet Polymer is as follows:
Polymer |
PolymerName |
{ |
|
ConstitutuveModel = |
"PowerLaw" |
|
Density = |
ρ |
|
SpecificHeat = |
Cp(T) |
|
Conductivity = |
K(T) |
|
CoeffOfThermalExpansion = |
βT |
|
VolumetricHeatSource = |
Qvol |
|
Consistency = |
A |
|
Exponent = |
n |
|
ZeroShearRate = |
γ0 |
|
TemperatureDependence = |
"None" } |
Parameter |
Description |
Units |
Data Type |
Condition |
Typical Value |
ConstitutiveModel |
Describes the model used |
None |
String |
Required |
"PowerLaw" |
Density |
Density of the polymer |
kg/m^3 |
Constant |
Required |
995.0 |
SpecificHeat |
Specific heat at constant pressure |
J/kg/K |
Constant / F(T) |
Required |
2000.0 |
Conductivity |
Thermal conductivity |
W/m/K |
Constant / F(T) |
Required |
0.167 |
CoeffOfThermalExpansion |
Indicates the change in volume with change in temperature |
1/K |
Constant |
Required |
1.0e-05 |
VolumetricHeatSource |
Heat generated/ removed in the volume by methods like electrical heating |
W/m^3 |
Constant |
Required |
0.0 |
Consistency |
One of the parameters of the power law model. When n=1 it is same as viscosity. |
Pa s^n |
Constant |
Required |
1.0e+04 |
Exponent |
Power law index, defines the dependency of viscosity on shear rate. |
None |
Constant |
Required |
0.66 |
ZeroShearRateLimit |
See above |
1/s |
Constant |
Required |
0.01 |
TemperatureDependence |
None |
String |
Required |
"Exp(-Beta(DeltaT))" |
|
ReferenceTemperature |
Temperature at which data is calculated for the initialization step. |
K |
Constant |
Required only if TD is not "None" |
533 |
FreezeTemperature |
This is the no flow temperature. Below this temperature, material ceases to flow. |
K |
Constant |
Required only if TD is not "None" |
350 |
ActivationEnergy |
A parameter required by Arrhenius model. |
J/mol |
Constant |
Required only if TD is Exp(Q/RT) |
16628 |
UniversalGasConstant |
A parameter from state equation PV = nRT, R is universal Gas constant. |
J/mol/K |
Constant |
Required only if TD is Exp(Q/RT) |
8.314 |
TemperatureSensitivity |
A derived parameter which has the same physical meaning as Q/R. |
K |
Constant |
Required only if TD is Exp(Tb/T) |
2000 K |
WLFConstant1 |
Constant C1 of WLF model |
None |
Constant |
Required only if TD is WLF |
17.44 |
WLFConstant2 |
Constant C2 of WLF model. This is like DeltaT, hence the value is same in K and Celsius. |
K |
Constant |
Required only if TD is WLF |
51.6 |
GlassTransitionTemperature |
Temperature below with polymer molecules ceases to move (frozen). There are few definitions of this term. |
K |
Constant |
Required only if TD is WLF |
320 |
Beta |
Parameter in the relationship Exp(-Beta(DeltaT)) |
None |
Constant |
Required only if TD is Exp(-Beta(DeltaT)) |
0.005 |
F(T) - Function of Temperature. Can be specified as a TABLE1 or TCL function.
TD - TemperatureDependence