Modeling Tools
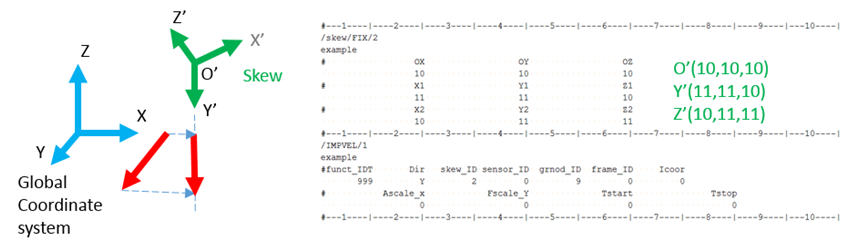
Skew and Frame (/SKEW & /FRAME)
Skews and frames are used to define local directions.
- Boundary conditions
- Concentrated load
- Fixed velocity
- Rigid link orientation
- Rigid body added inertia frame
- General spring reference frame
- Beam type spring initial reference frame
- Nodal time history output frame
- Skew reference
- It is a projection reference to define the local quantities with respect to the global reference. In fact, the origin of the skew remains at the initial position during the motion even though a moving skew is defined. In this case, a simple projection matrix is used to compute the kinematic quantities in the reference.
- Frame reference
- It is a mobile or fixed reference. The quantities are computed with respect to the origin of the frame which may be in motion or not depending on the kind of reference frame. For a moving reference frame, the position and the orientation of the reference vary in time during the motion. The origin of the frame defined by a node position is tied to the node.
Sections (/SECT)
A section is used to measure the force, moment, and energy which are passing through a set of elements and nodes. The section displacements can also be saved to a file and used as imposed displacements in a smaller cut section model.
- A group of nodes and groups of elements. The nodes and elements can be selected by a user in /SECT. They can also be automatically selected by defining a section cut using /SECT with frame_ID, /SECT/PARAL, or /SECT/CIRCLE.
- A local output system defined by selecting 3 points
- A reference point to compute forces and moment
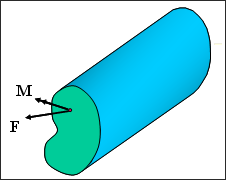
Figure 3. Definition of a Section for an Oriented Solid
Section Cutting Plane
In /SECT, the cutting plane is infinite and is defined by a group of elements and a group of nodes. The elements and nodes can be user-defined and should be along one row, if possible.
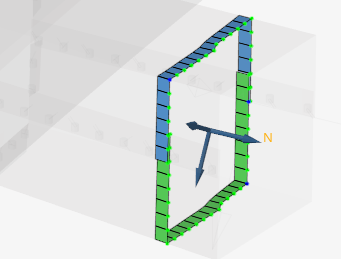
Figure 4. Elements and Nodes Selected Manually
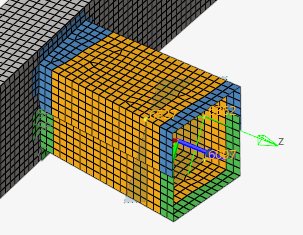
Figure 5. Element Group (in orange) defined for a section cut defined using a local system
NUMBER OF NODES. . . . . . . . . . 40
NODES:
6062 6064 6055 6074 6076 5895 6078 6173 6166 6136
6174 6181 6182 6219 6210 6220 6227 6228 6359 6358
...
NUMBER OF SHELL ELEMENTS . . . . . 43
SHELL N1 N2 N3 N4
5819 0 1 1 0
5820 0 1 1 0
5826 0 0 1 0
5839 0 1 1 0
...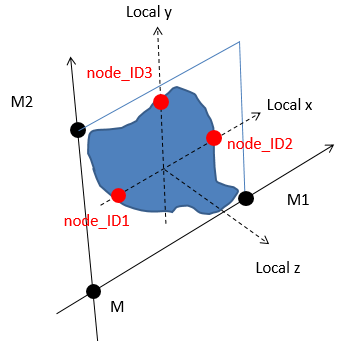
Figure 6. /SECT/PARAL Definition
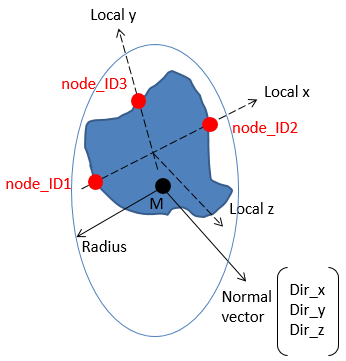
Figure 7. /SECT/CIRCLE Definition
All section types can cut solid, shell, truss, beam, and spring elements. Contact interfaces can also be selected.
When using /SECT with frame_ID, /SECT/PARAL, or /SECT/CIRCLE the nodes used for the section calculation will on the +z side of the selected elements. Since these nodes are automatically defined, the element groups can be defined by part and; thus, will not need to be redefined, if the part is re-meshed.
Local System of Cutting Plane
A local system must be defined to compute the force and moment from the section.
- Nodes node_ID1 and node_ID2 define the local x-axis of the section.
- Nodes node_ID1, node_ID2, and node_ID3 define the local plane xy of the section.
- The local y-axis is defined by projecting node_ID3 perpendicular to the local x-axis.
- The intersection of the local x- and y-axis is then the origin of the system.
- The section normal is the local z-axis which is perpendicular to the xy plane.
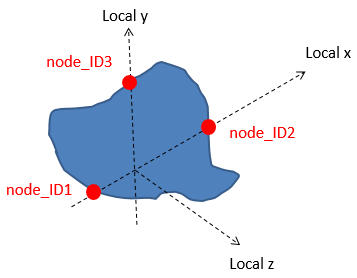
Figure 8. Section local system defined using nodes
When creating a /SECT in HyperMesh, these three nodes are automatically selected for the user. If they are manually selected, it is recommended to select nodes that belong to the group of nodes used in the section calculation. This will allow the local system to move as the section deforms.
Alternatively, in /SECT if the 3 nodes are not defined and instead a frame_ID is defined, the xy plane of the /FRAME/MOV is used as the local system. When defining the /FRAME/MOV, it is recommended to use nodes that belong to the group of nodes used in the section calculation.
Force and Moment Computation
The section force is the sum of nodal force coming from the selected elements.
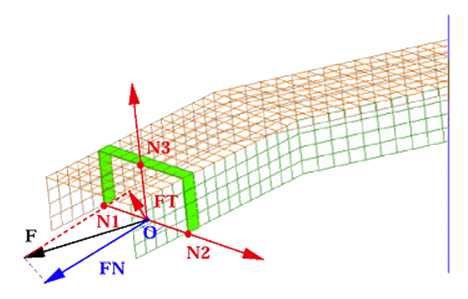
Figure 9. Normal section force and tangent section force in section
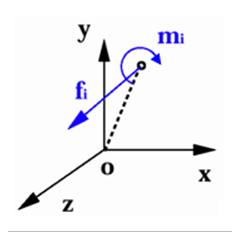
Figure 10. Resultant of force and moment for a node
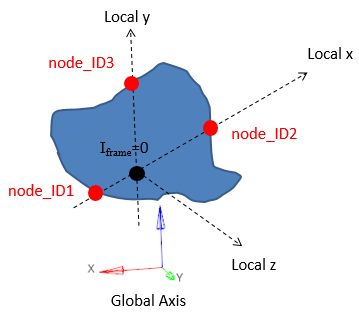
Figure 11. Iframe=0 Local system and origin used for section output
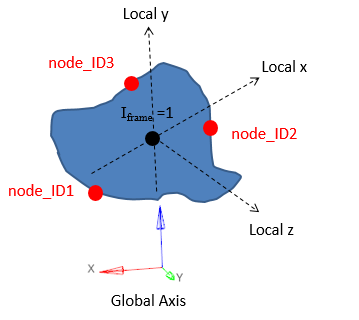
Figure 12. Iframe=1 Local system with the origin as the geometric center of the section
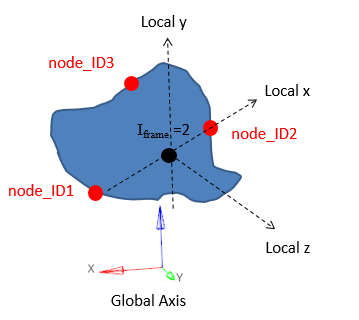
Figure 13. Iframe=2 Local system with the origin as the center of gravity of the section
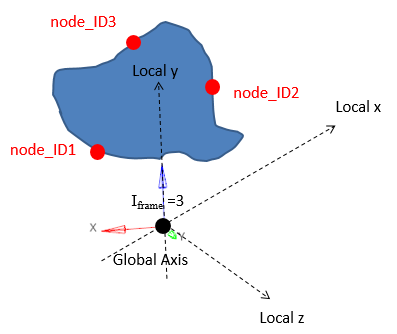
Figure 14. Iframe=3 Local system with the global origin as the center
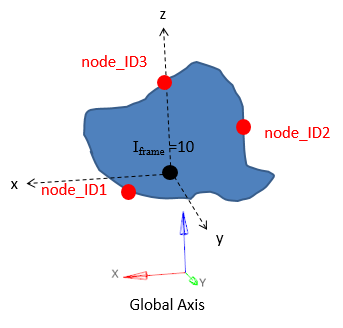
Figure 15. Iframe=10 Global system with the center as the local system origin
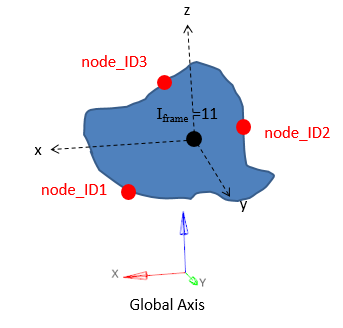
Figure 16. Iframe=11 Global system with the origin as the geometric center of the section
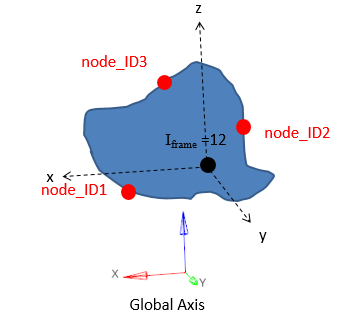
Figure 17. Iframe=12 Global system with the origin as the center of gravity of the section
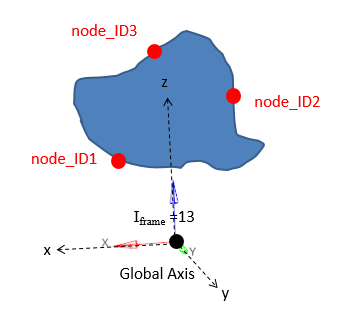
Figure 18. Iframe=13 Global system with the global origin as the center
Output of Section
Two types of section output are available.
First is the time history output /TH/SECTIO consisting of the sum of the force and moments acting on the section. The output can be in the global system or the local system with the most commons output being the variable groups, GLOBAL, LOCAL, and CENTER.
The second type of output is displacements and optional force and moment for every node in the section written to the section output data SC01 file. This file can then be read as an imposed displacement applied to a second cut section model. RD-E: 5400 Cut Methodology is an example of the cut section methodology that can be used. In this case, a full model is run with ISAVE=1 or 2 to save displacement and optionally the resultant section forces/moments in the file file_nameSC01.
Next, the second cut model (submodel) is created with a section defined using the option ISAVE=100 or 101 to read the displacement of the nodes the section file. The section’s local system defined by the three nodes node_ID1, node_ID2, and node_ID3 or frame_ID must be the same one used when saving the data (ISAVE=1 or 2) and reading the data (ISAVE=100 or 101).
If ISAVE=2 is used in the full model and ISAVE=101 is used in the cut model, then Radioss outputs the difference between resultant section forces and moments in full and cut model in the section (/TH/SECTIO).
To improve solution times and decrease memory needed, it is recommended to set ISAVE =0 if no cut modeling methodology is needed.
Filter
- Filtered displacement
- Exponential moving average filtering constant
- Unfiltered displacement at the current time
- Displacement at the previous time step
Recommendations are:
for filtering -3dB
for filtering -6dB
- Filtering period
- Model time step
The filtering period is often used making for a -3dB filter.