mscohere
Estimates the mean squared coherence of time domain signals.
Syntax
msc=mscohere(x,y)
msc=mscohere(x,y,window)
msc=mscohere(x,y,window,overlap)
msc=mscohere(x,y,window,overlap,nfft)
msc=mscohere(x,y,window,overlap,nfft,fs)
msc=mscohere(x,y,window,overlap,nfft,fs,range)
[msc,freq]=mscohere(...)
Inputs
- x
- The signal.
- window
- The window size, or the window vector.
- overlap
- The number of overlapping points in adjacent windows.
- nfft
- The size of the fft.
- fs
- The sampling frequency.
- range
- The spectrum type: 'onesided' or 'twosided'.
Outputs
- msc
- The mean squared coherence.
- freq
- The vector of frequencies corresponding to the coherence values.
Example
Coherence of two signals sharing common frequency components.
n = 4096;
fs = 256;
ts = 1/fs;
t = [0:ts:(n-1)*ts];
w1 = 2*pi*20;
w2 = 2*pi*32;
w3 = 2*pi*48;
w4 = 2*pi*60;
signal1 = 5*cos(w1*t) + 7*cos(w2*t) + 3*cos(w4*t);
signal2 = 7*cos(w1*t + (pi/2)) + 5*sin(w3*t) + 2*cos(w4*t + pi);
rand('seed', 2019);
signal1 = signal1 + randn(1, n);
signal2 = signal2 + randn(1, n);
window = ones(1, 64);
mscohere(signal1, signal2, window, 0, [], fs);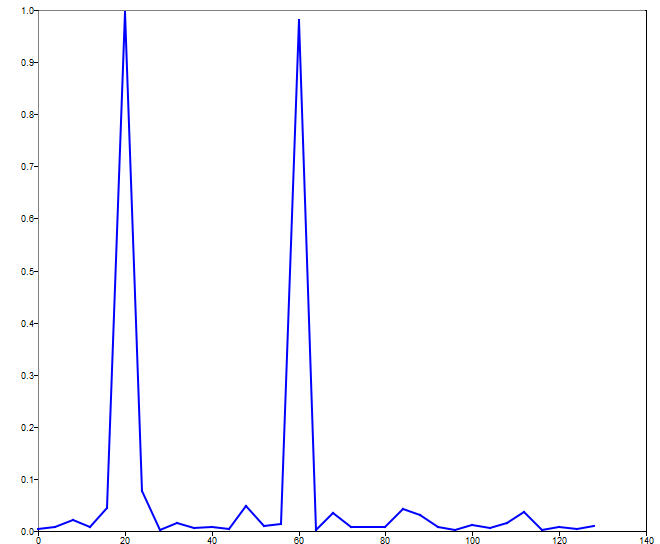
Figure 1. impz figure 1
Comments
With no return arguments, the function will automatically plot.
The 'onesided' output has a length of nfft/2+1 if nfft is even, or (nfft+1)/2 if nfft is odd.
It is often recommended to remove the signal means prior to calling mscohere. The function does not remove the mean automatically.
- window
- A Hamming window with the largest length that produces eight data segments.
- overlap
- One half of the window length.
- nfft
- The window length. A larger value will pad zeros to each block of windowed data.
- fs
- 1.0 Hz.
- range
- 'onesided'