Block Category: Matrix Operation
Description: The ifft block converts data from frequency domain to time domain. The ifft block computes an n-sample inverse FFT at every simulation time step, where n is the length of the input vector.
If the input to the ifft block is not an integral power of 2, automatic zero padding is performed to make the input vector size an integral power of 2. This is a standard procedure in inverse FFT computation. The output of the ifft block is Fourier coefficients. Individual coefficients can be accessed using a vecToScalar block.

Label: Indicates a user-defined block label that appears when View > Block Labels is activated.
1. Computation of FFT and inverse FFT
Consider a simple example, where a sinusoidal signal is converted to frequency domain via FFT, and then reconstructed using inverse FFT.
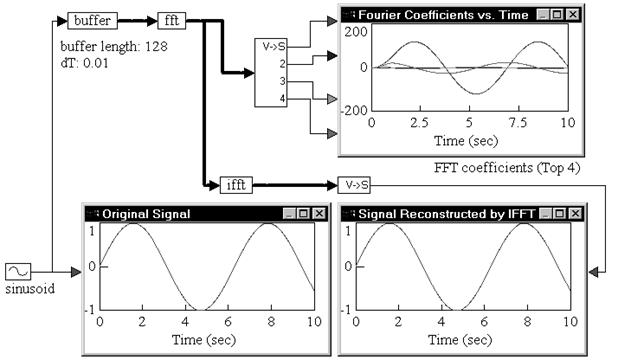
A sinusoid block generates a sinusoid signal with a frequency of 1 rad/sec. The signal is passed through a buffer block of length 128 samples and a sampling rate of 0.01. The output of the buffer block is connected to an fft block, which computes a 128-sample FFT of the original sinusoid at a sampling rate of 0.01.
The output of the fft block is Fourier coefficients. The individual coefficients are accessed using a vecToScalar block. The first four coefficients are plotted to show their variation with time.
Signal reconstruction is performed by feeding the output of the fft block to an ifft block to compute the inverse FFT. The output of the ifft block is a vector of length 128 samples. The contents of this vector are just 128 sinusoid reconstructions, with each sinusoid trailing the preceding sinusoid by an amount equal to the sampling rate.
The first element in the ifft output vector does not have any delay because zero time has elapsed between the FFT and inverse FFT phases. In most real-world situations, however, there is a small, non-zero delay between the input signal and its reconstruction that is introduced by the processor performing the numerical computations of FFT and inverse FFT algorithms.