Modeling of magnetic materials by Amperian currents
Introduction
In order to introduce the magnetic materials in the standard PEEC approach, the most efficient technique seems to be the modeling by Amperian currents, as it preserves the same structure of the equivalent circuits R, L and M described in the previous sections.
The principles, as well as some equations on the Amperian currents model, are given in the following sections.
Principle
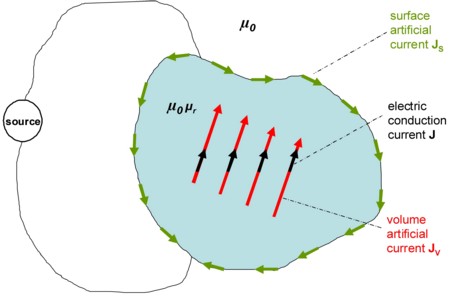
The Amperian currents modeling consists in reproducing the effects of the magnetization M of magnetic bodies by an equivalent distribution of artificial currents, permitting therefore to place the equipment in the context of vacuum magnetism.
In practice it is the same concept of electrostatics, which consists in replacing the effects of the polarization P of dielectric bodies by an equivalent distribution of artificial electric charges.
Magnetic vector potential
The expression of the magnetic vector potential A created in a point by a conductive body V' crossed by a current and characterized by the local magnetization M is different from the similar expression for a non-magnetic body. The additional contribution of the magnetization M must be taken into consideration as well:
![]()
By vector analysis relationships and the theorem of Stokes this contribution is rewritten under the following form:
![]()
where ![]() is the normal
getting out to the surface S' of the conductor.
is the normal
getting out to the surface S' of the conductor.
The contribution Am to the magnetic vector potential A can therefore be interpreted as the potential created by two artificial currents:
- one volume current
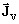 , characterized by the current density
, characterized by the current density 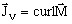
- one surface current
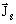 , characterized by the current density
, characterized by the current density 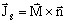
The physical interpretation of these two currents is explained in the following sections.
Artificial volume current density 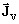
According to their definition ![]() , these
currents can be seen as current loops located at the inner part of
the magnetic conductor. Consequently, they do not participate in
the macroscopic electric conduction or they are not involved in
generation of losses by the Joule effect. These two phenomena are
associated exclusively to the electric conduction currents.
, these
currents can be seen as current loops located at the inner part of
the magnetic conductor. Consequently, they do not participate in
the macroscopic electric conduction or they are not involved in
generation of losses by the Joule effect. These two phenomena are
associated exclusively to the electric conduction currents.
Conversely, they generate magnetic fields, which means that they increase the magnetic flux density B and therefore the magnetic vector potential A with respect to the values generated by the electric conduction currents.
Under the hypothesis that the materials are magnetic linear and therefore that the effects of magnetic saturation and hysteresis are neglected, the expression of the artificial volume current density becomes:
![]()
where ![]() is the electric
conduction current.
is the electric
conduction current.
Artificial surface current density 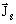
The artificial surface currents of density ![]() enable the closing of the artificial
volume currents of density
enable the closing of the artificial
volume currents of density ![]() .
.
Indeed, as the ![]() currents do not participate in the macroscopic electric
conduction and as they cannot close by the external circuit, it is necessary to
introduce surface currents to guarantee that there is no electric charge accumulation at
the surface of the conductor.
currents do not participate in the macroscopic electric
conduction and as they cannot close by the external circuit, it is necessary to
introduce surface currents to guarantee that there is no electric charge accumulation at
the surface of the conductor.
This principle is illustrated in the figure below.