Transformation: about

Principle of use

The transformations are geometric functions that permit the creation of new objects, starting from objects already created.

Various functions

The various available functions are:

  • translation
  • rotation
  • affinity included symmetry
  • composed transformation

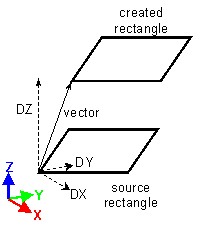
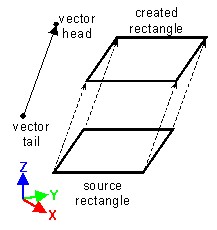
Translation

A translation is defined by a direction and a distance.
Translation vector Translation defined by two points and a ratio
  • the direction and the distance are defined by:
    • a working coordinate system
    • a vector (its components DX, DY and DZ define the direction and the amplitude of the vector)
  • the direction is defined by two points (vector tail and vector head)
  • the distance is proportional to the distance between the two points (vector tail and vector head) calculated with the scaling factor (ratio)

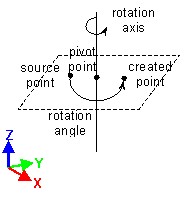
Rotation

A rotation is defined by a rotation axis and an angle.

Rotation defined by three angles and a pivot point
  • rotation axis and angle are defined by:
    • a working coordinate system
    • a pivot point
    • and rotation angles are defined around X, Y and Z axis

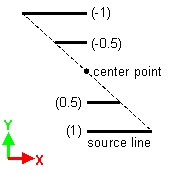
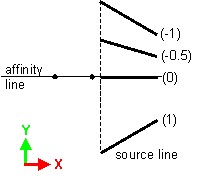
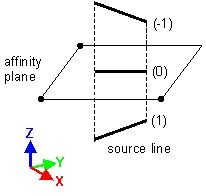
Affinity

Affinity is defined with respect to a point, to a straight line or to a plane.

The result of this transformation application depends on the affinity ratio (see the table below).

Ratio Result
k = -1 symmetry
k = 1 identity
k = 0 projection
k > 1 increasing (increasing affinity)
0 < k < 1 reducing (reducing affinity)
k < -1 increasing (increasing negative affinity)
-1 < k < 0 reducing (reducing negative affinity)
Affine transformation with respect to a point Affine transformation with respect to a line Affine transformation with respect to a plane
Warning: The scaling factor of affine transformation k = 0 causes an error in the application when the affine transformation with respect to a point is applied, because the concerned geometric entity (point, line, face or volume) is already created (in the case of a point) or degenerated and reduced to a point (in the case of a line, face or volume).

Symmetry

A symmetry is a particular case of affine transformation when k = -1 (see above); it is defined with respect to a point, a line or a plane.

Composed transformation

It is possible to create composed transformation combining the two already created transformations.

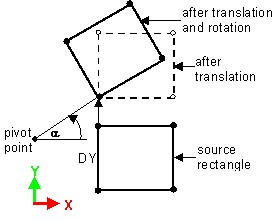
Transformation combining two transformations:

  • a translation following Y-axis (defined by DX=0, and DY)
  • a rotation about Z-axis (defined by the pivot point and an angle α)
Warning: You do not obtain the same result by using different order of two transformations.

Parameter setting

The characteristics of transformation are parametrized expressions. The vector components, the coordinates of pivot point, the rotation angles and the ratios of affinity can be defined using algebraic expression.

The algebraic expression can contain:

  • constants
  • geometric parameters (created beforehand)
  • basic mathematical functions using operators: +, -, *, /, ( )
  • usual mathematical functions admitted by FORTRAN

The mathematical functions are described in section Functions.