Electro Statique : équations résolues
Introduction
Dans une application Electro Statique, les équations utilisées pour la résolution sont :
- les équations de Maxwell (pour un système électrique)
- les équations constitutives de la matière, caractérisant les matériaux diélectriques
Les conditions de calcul pour une application Electro Statique sont les suivantes :
- on s'intéresse aux champs D et E (les champs B et H ne sont pas calculés). Les équations en champs électriques E, D et en champs magnétiques B, H sont découplées
- les champs sont indépendants du temps (statique) : d/dt = 0
- la densité de courant est nulle : J = 0
Equations et conditions
| Equations | Description | |
|---|---|---|
|
E : champ électrique (en V/m) D : induction électrique (en C/m2) V : potentiel électrique (en V) q : densité de charges électriques (en C/m3) |
|
|
εr : permittivité
relative ε0 : permittivité du vide (en F/m) |
|
Equation résolue
L'équation résolue par la méthode des éléments finis dans une application Electro Statique est l'équation suivante :
![]()
où:
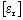 est le tenseur de
permittivité relative du milieu
est le tenseur de
permittivité relative du milieu- ε0 est la permittivité du vide ; ε0 = 1/(36π109) (en F/m)
- V est le potentiel électrique (en V)
- q est la densité de charges électriques (en C/m3)
Variable d'état
La variable d'état de l'application Electro Statique est le potentiel électrique V (noté Ve dans Flux 3D).
Pour que le potentiel V soit entièrement défini, il faut imposer ce potentiel au moins en un point.