Magnéto Harmonique : équations résolues (introduction)
Introduction
Les équations utilisées pour la résolution sont :
- les équations de Maxwell (pour un système magnétique)
- les équations constitutives de la matière
Les conditions de calcul pour une application Magnéto Harmonique sont les suivantes :
- l'étude est une étude temporelle : d/dt ≠ 0 (régime permanent sinusoïdal : les sources de courant varient sinusoïdalement en fonction du temps).
-
on s'intéresse aux champs B, H et E (le champ D n'est pas calculé).
Les équations en champs magnétiques B, H et en champs électriques E, D ne peuvent pas toujours être découplées.
Equations et conditions
Dans les conditions de calcul énoncées précédemment, les équations se résument de la façon suivante :
|
|
E : champ électrique (en V/m) B : induction magnétique (en T) H : champ magnétique (en A/m) J : densité de courant (en A/m2) |
|
|
σ : conductivité du milieu (en S) μ : perméabilité du milieu (en H/m) |
L'équation constitutive de la matière pour les matériaux magnétiques, peut se mettre sous la forme B(H) ou H(B) comme présenté ci-dessous.
|
|
⇒ |
|
μr : perméabilité relative μ0 : perméabilité du vide |
|
|
⇒ |
|
νr : réluctivité νr =1/μr ν0 : réluctivité du vide ν 0 =1/μ0 |
Les modèles
Pour résoudre ces équations, deux modèles sont utilisables :
-
le modèle vecteur qui utilise :
le potentiel vecteur magnétique (noté
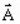 )
) -
le modèle scalaire qui utilise :
des potentiels scalaires magnétiques (notés ϕtot ou ϕred)
Modèle et application 2D ou 3D
Les deux modèles (vecteur et scalaire) sont proposés :
- le modèle vecteur pour les applications 2D
- le modèle scalaire pour les applications 3D