Isovaleurs: à propos
Tracé d'isovaleurs
Les grandeurs spatiales scalaires peuvent être visualisées sous forme d'isovaleurs en dégradés de couleurs sur différents supports.
Pour les grandeurs spatiales vectorielles, aussi bien le module que les composantes peuvent être affichées sous forme d'isovaleurs.
Le support
Le support pour le tracé d'isovaleurs est toujours un support surfacique. Dans Flux PEEC les supports disponibles sont :
- les surfaces externes des conducteurs unidirectionnels
- les surfaces externes des conducteurs bidirectionnels
- les grilles 2D
L'algorithme de calcul
Le calcul du tracé d'isovaleurs est effectué en deux étapes :
- d'abord, la grandeur spatiale considérée est calculée à certains points
caractéristiques des surfaces de support ; ces points dépendent de la grandeur
spatiale considérée, mais d'une manière générale sont très liés à :
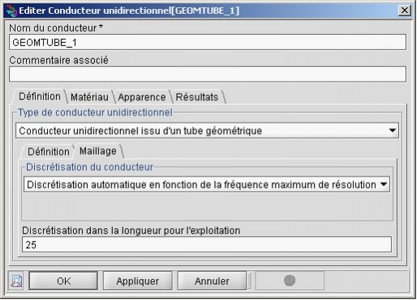
- pour les conducteurs unidirectionnels, au maillage et aux points de discrétisation supplémentaires rajoutés dans la direction de la longueur uniquement pour l'exploitation des résultats *
- pour les conducteurs bidirectionnels, au maillage
- pour les grilles 2D, à leur propre discrétisation, comme décrit dans § Grilles 2D : à propos
- ensuite, un algorithme d'interpolation permet le calcul de la grandeur considérée aux points intermédiaires et donc le lissage du tracé des isovaleurs
Les grandeurs spatiales
Les grandeurs spatiales qui peuvent être affichées sous forme d'isovaleurs sont :
- le module et les trois composantes (selon X, Y ou Z) de la densité de courant
- la densité des pertes par effet Joule
- le module et les trois composantes (selon X, Y ou Z) de l'induction magnétique
- le module et les trois composantes (selon X, Y ou Z) de la densité de force de Laplace : aussi bien la composante moyenne que la composante pulsatoire à 2ω