Latin HyperCube

An approach which can yield precise estimates of output statistics with a lesser number of samples than simple random sampling.

The Latin HyperCube method uses a constrained or stratified sampling scheme.

Latin HyperCube sampling selects n different values from each of k variables x 1 , … x k in the following manner:
  • The range of each random variable is divided into n non-overlapping intervals on the basis of equal probability.
  • One value from each interval is selected at random with respect to the probability density in the interval.
  • The n values thus obtained for x 1 are paired in a random manner with the n values of x 2 . These n pairs are combined in a random manner with the n values of x 3 to form n triplets and so on, until n k-tuplets are formed.


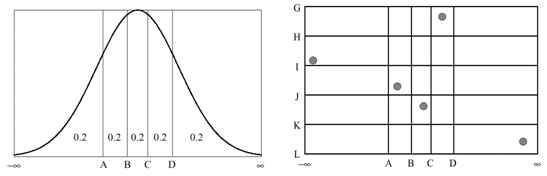
Figure 1. Latin HyperCube Sampling

Usability Characteristics

  • A stratified sampling scheme like Latin HyperCube offers the advantage of selecting random variable values that are uniformly spread across the range of random variables while taking into account the probability density function of those random variables.
  • A correlation structure can be specified to reflect the correlation existing between random variables. Applying a correlation structure can be costly for a large number of input variables.

Settings

In the Specifications step, Settings tab, change method settings.
Parameter Default Range Description
Number of Runs 100 > 0 Number of new designs to be evaluated.
Random Seed 1 Integer

0 to 10000
Controlling repeatability of runs depending on the way the sequence of random numbers is generated.
0
Random (non-repeatable).
>0
Triggers a new sequence of pseudo-random numbers, repeatable if the same number is specified.
Apply User Correlations On Off or On Apply user specified correlations on the data.