Moving Least Squares Method (MLSM)
Builds a weighted least squares model where the weights associated with the sampling points do not remain constant.
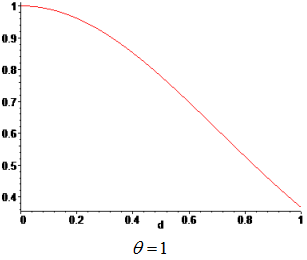
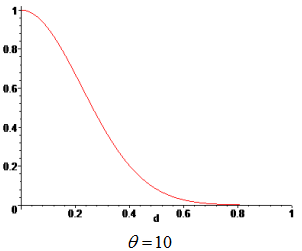
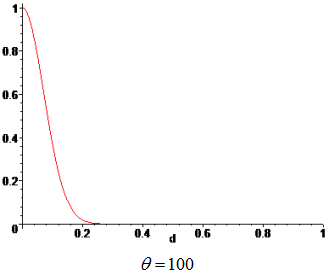
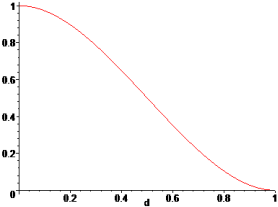
Weights are functions of the normalized distance from a sampling point to a point x, where the surrogate model is evaluated. The weight, associated to a sampling point, decays as the evaluation point moves away from it. The decay is defined through a decay function. For each point x it reconstructs a continuous function biased towards the region around that point.
Usability Characteristics
- Suggested to be used for nonlinear and noisy output responses.
- Residuals and diagnostics should be used to gain an understanding of the quality of the Fit.
- Use a Testing matrix in addition to an Input matrix for better diagnostics.
- Quality of a Moving Least Squares Method Fit is a function of the number of runs, order of the polynomial and the behavior of the application.
- If the residuals and diagnostics are not good for a Moving Least Squares Method Fit, than you can increase the order of the Fit provided you have enough runs to fit that specific order.
- Because the weights are not constant in Moving Least Squares Method, there is no analytical form and an equation can not be provided.
Settings
| Parameter | Default | Range | Description |
|---|---|---|---|
| Fit Parameter | 5.0 |
|
Controls the effect of screening out noise; the larger value, the less effect. |
| Minimum Weight | 0.001 | > 0.0 | Minimum weight. |
| Number of Excess Points | 3 | >=0 | Number of excessive points to build Moving Least Squares Method. |
| Regression Model | Linear |
|
Order of polynomial function. |
| Weighting Function | Gaussian |
|
Type of weighting function.
|