Interactions Post Processing

Measure the result of two variables moving simultaneously.

Analyze Interactions

Analyze the effect of an input variable on an output response at varying levels of other input variables in the Interactions post processing tab.

An interaction is the failure of one input variable to produce the same effect on the output response at different levels of another input variable. In other words, the strength or the sign (direction) of an effect is different depending on the value (level) of some other variable(s). An interaction can be either positive or negative.

  1. From the Post Processing step, click the Interactions tab.
  2. Using the Channel selector, select the input variable(s) and output response(s) to analyze.
  3. Change the format to display interactions by switching the view between (Interactions Plot) and (Interactions Table).
  4. Analyze interactions.
Tip: Display selected data in a single plot or separate plots by switching the Multiplot option between (single plot) and (multiple plots).

Example: Interactions

In Table 1, interactions are calculated as:
  • Effect of X when Y = +1 is (401 - 401) / 2 = 0
  • Effect of X when Y = -1 is (1601 - 1) / 2 = 800
Interaction of X on Y is then (0 - 800) = -800
  • Effect of Y when X = +1 is (401 - 1601) / 2 = -600
  • Effect of Y when X = -1 is (401 - 1) / 2 = 200
Interaction of X on Y is then (-600 - 200) = -800
Table 1. Design Matrix
Run X Y F(X,Y)
1 0 0 1
2 0 2 401
3 2 0 1601
4 2 2 401
Interactions are symmetric; that is:
  • Interaction XY = effect of (X) on effect of (Y) = effect of (Y) on effect of (X)


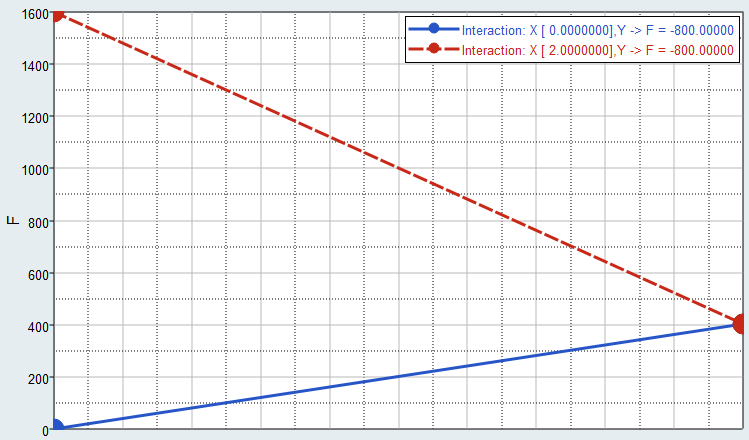
Figure 1. Interactions Plot


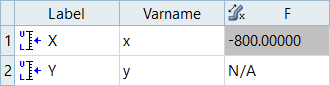
Figure 2. Interactions Table
Note: HyperStudy calculates interactions using a regression based on the data set. In this example, the regression is f(x,y) is ao+a1*x+a2*y+a3*x*y; where a3 is equal to -400.0 and x and y are between -1.0 and 1.0. The interaction of the input variables x and y on the output response f(x,y) is -800.0.