放物線方程式法

放物線方程式法は、不均質な地形における回折および前方散乱プロセスを効率的に記述します。

経験的モデルでは精度が制限されるため、不均質な地形における回折および前方散乱プロセスと、大規模変動に対する地形の影響を記述する方法が必要になります。このため、さまざまな全波アプローチが研究され、その中で考えられた1つの効率的な方法が放物線方程式法です。

この方法は、地形データに基づいてマクロセル領域の電磁界強度を計算するために、放物線方程式（PE）の数値評価を採用しています。さまざまな伝搬メカニズム（自由空間伝搬、反射、回折）が暗黙的に考慮されているので、このモデルは非常に高精度になっています。高度なアルゴリズムなので、経験的モデルと比べて計算時間は非常に長くなります。

基本原理

図 1 は、PEモデルの垂直地形セクションと計算領域を示しています。



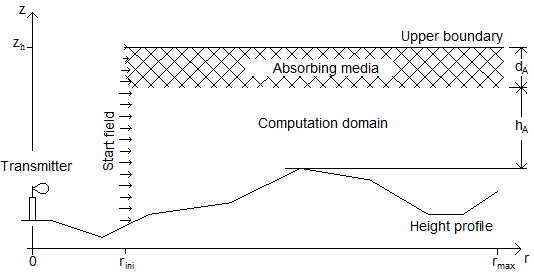
図 1. 垂直地形セクションと計算領域

後方伝搬を無視し、回転対称問題を想定することで、Maxwell方程式から放物線タイプの偏微分方程式を求めることができます。

(1) ∂ Ψ ∂ r + j 2 k 0 ⋅ ∂ 2 Ψ ∂ z 2 + j ⋅ k 2 − k 0 2 2 ⋅ k 0 ⋅ Ψ = 0
(2) E z = Z F 0 ⋅ H Φ ψ r ⋅ e −j k 0 r

このいわゆる標準放物線方程式（SPE）は、水平線を基準とする伝搬角度が–15°～15°の範囲にある場合に有効な結果を導き出します。したがって、PEを送信機の近くで使用することはできません。

有限差分法では、反復手法を使用して計算領域内でPEを解析します。WinPropでは、 r ini の必要な開始電界が、自由空間伝搬と1つの地面反射レイを使用して計算されます。

吸収媒質

計算領域の上部で透明境界条件を実装すると計算時間が長くなってしまうため、代わりに吸収媒質を使用して上方境界での反射を防止します。幅をおよそ dA=150 波長にすると、最も高い地形ポイントまでの適正距離を hA だと想定した場合、この吸収媒質はすべての周波数に対して十分に機能します。

図 2の予測プロットでは、点線より上で人工的な吸収媒質内の電界を示しています。



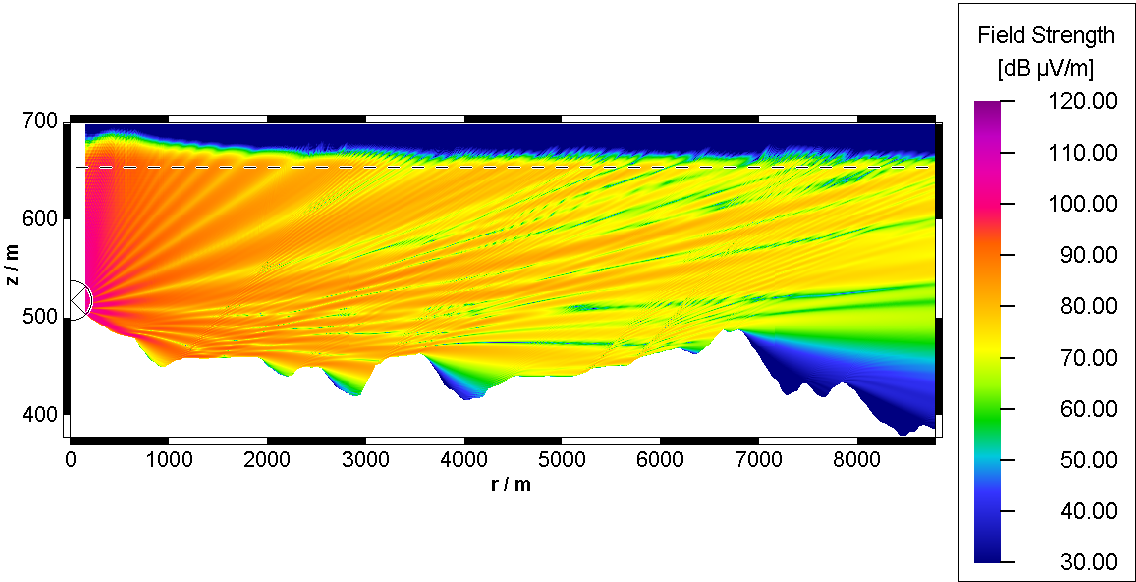
図 2. 予測の例（945MHz、垂直地形セクション）

地面のインピーダンス境界

すべての放物線方程式の計算で、地表面の導電率と誘電率が考慮に入れられます。インピーダンス境界条件をモデル化する方法の3つのバリエーションをここに示します。

  1. 個別の地形近似

    図 3では階段状の高さプロファイルが想定されており、これにより簡素化されたLeontovich境界条件がもたらされます。

    (3) Ψ z +αΨ=0
    (4) α=−j k 0 1 ε r eff


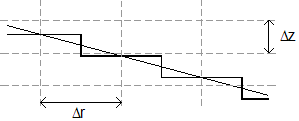
    図 3. 階段状の高さプロファイルの近似

    この方法は数値的に不安定なので、下り坂の地面では計算グリッドの放射ステップサイズ △r が自動的に削減されます。

  2. 連続する地形近似

    複素波数 k に適切な値を設定することで、大気の一部のように地面をモデル化します。可変ステップサイズ △r と合わせることで、このアプローチは非常に堅牢になりますが、放物線近似の使用時には空中媒質の突然の変更が許可されないので、境界条件には必ずしも一致しません。

  3. 座標変換による地形プロファイル近似

    数値的不安定さを回避するために考えられるもう1つの方法は、下り坂の地面に対して、図 4に示すように不規則な計算領域を長方形の領域に変換する方法です。



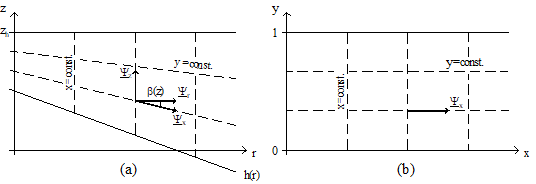
    図 4. 計算領域の変換

    したがって、次のような座標変換が行われます。

    (5) x=r
    (6) y= z−h( r ) z h −h( r )
    (7) Ψ z cos( θ )+( −j k 0 sin| θ |+α )Ψ=0

    計算グリッドに歪みがあるため、この変換はわずかに小高い地形に対してしか使用できません。

広角放物線方程式

有効な伝搬角度が小さいという標準放物線方程式の欠点は、Maxwell方程式の拡張型放物緯線近似を使用すると矯正できます。

これによって、およそ40°までの伝搬角度が許容されるようになります。追加の項によって計算時間が長くなることはほとんどないので、広角PEを優先するようにしてください。