Aimant (vectoriel) : approximation linéaire
Présentation
Ces modèles ( Aimant linéaire décrit par le vecteur cartésien / cylindrique / sphérique Br ) permettent de définir une courbe de désaimantation B(H) linéaire dans Flux (non disponible dans le gestionnaire de matériaux).
Caractéristiques principales :
- le modèle mathématique et la direction d'aimantation sont associés
- autant de matériaux et/ou de repères que de régions
Modèle mathématique
Dans la direction d'aimantation , le modèle est une droite .
La formule mathématique correspondante s'écrit :
Β(Η)=μ0μr Η+ Br
où:
- μ0 est la perméabilité du vide ; μ0 = 4 π 10-7 (en H/m)
- μr est la perméabilité relative (droite de recul)
- Br est l'induction rémanente (en T)
L'allure de la courbe B(H) est représentée sur la figure ci dessous :
Direction d'aimantation
La direction d'aimantation est «associée» au modèle. Trois modèles sont proposés : vecteur cartésien, cylindrique ou sphérique.
Aimantation cartésienne
Le modèle mathématique est le modèle linéaire décrit précédemment.
La caractéristique B(H) est définie par la relation
suivante dans un repère cartésien : ![]()
où :
-
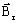 est l'induction rémanente définie par 3 composantes suivant les 3 axes du repère
cartésien : ( Brx , Bry , Brz )
est l'induction rémanente définie par 3 composantes suivant les 3 axes du repère
cartésien : ( Brx , Bry , Brz ) - μr est le tenseur de perméabilité relative défini sur les 3 axes du repère cartésien : ( μrx , μry , μrz )
Aimantation cylindrique
Le modèle mathématique est le modèle linéaire décrit précédemment.
La caractéristique B(H) est définie par la relation suivante dans un repère cylindrique
: ![]()
où :
-
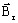 est l'induction rémanente définie par 3
composantes
est l'induction rémanente définie par 3
composantessuivant les 3 axes du repère cylindrique : ( Brr, Brθ et Brz)
- μr est la perméabilité relative
| radiale (Brr) | orthoradiale (Brθ) | axiale (Brz) |
|---|---|---|
|
|
|
|
Aimantation sphérique
Le modèle mathématique est le modèle linéaire décrit précédemment.
La caractéristique B(H) est définie par
la relation suivante dans un repère sphérique : ![]()
où :
-
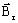 est l'induction
rémanente définie par 3 composantes suivant les 3 axes du repère sphérique : (
Brr, Brθ et Brφ )
est l'induction
rémanente définie par 3 composantes suivant les 3 axes du repère sphérique : (
Brr, Brθ et Brφ ) - μr est la perméabilité relative
radiale (Brr)