Magnéto Statique : équations résolues (modèle scalaire)
Introduction
Le modèle scalaire est le modèle général proposé pour une application 3D.
Ce modèle est utilisé par défaut (en automatique) par le solveur 3D de Flux 3D pour la résolution d'une application 3D.
Equation résolue en modèle scalaire (3D)
L'équation ![]() permet
d'introduire différents potentiels scalaires magnétiques ϕ tels que :
permet
d'introduire différents potentiels scalaires magnétiques ϕ tels que : ![]() . La partie
. La partie ![]() est une partie
irrotationnelle du champ
est une partie
irrotationnelle du champ ![]() (
( ![]() ) tandis que la
partie
) tandis que la
partie ![]() peut être de
rotationnel non nul.
peut être de
rotationnel non nul.
![]() peut être choisi
de différentes façons et un choix différent de
peut être choisi
de différentes façons et un choix différent de ![]() conduit à un potentiel scalaire différent.
Flux 3D dispose de formulations magnétiques
différentes utilisant des potentiels scalaires
différents. A chaque région du problème correspond
une formulation et par conséquent une équation.
conduit à un potentiel scalaire différent.
Flux 3D dispose de formulations magnétiques
différentes utilisant des potentiels scalaires
différents. A chaque région du problème correspond
une formulation et par conséquent une équation.
La forme générale de l'équation résolue par la méthode des éléments finis dans une application magnétostatique s'écrit:
![]()
où:
- [μr] est le tenseur de perméabilité magnétique relative du milieu
- μ0 est la perméabilité magnétique du vide ; μ0 = 4 π 10-7 (en H/m)
- ϕ est un potentiel scalaire magnétique (en A) : ϕtot ou ϕred
-
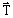 est un terme
correspondant aux sources (champ source ou potentiel vecteur électrique (en
A/m))
est un terme
correspondant aux sources (champ source ou potentiel vecteur électrique (en
A/m)) 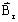 est l'induction
rémanente (aimants) (en T)
est l'induction
rémanente (aimants) (en T)
Les formulations proposées…
Les trois formulations proposées dans le modèle scalaire correspondent schématiquement aux trois situations suivantes :
- il n'y a pas de source de courant
- les sources de courant sont des sources non maillées
- les sources de courant sont des sources maillées
Les équations résolues dans ces trois situations sont présentées ci-après.
Utilisées de manière isolée, chacune de ces formulations présente des limitations importantes; utilisées de manière couplée, elles forment un modèle général performant.
Le potentiel scalaire total (3D)
Le potentiel scalaire magnétique total, ϕtot, est utilisé dans le cas où il
n'y a pas de sources de courant. La densité de courant ![]() est nulle, ce qui
correspond à
est nulle, ce qui
correspond à ![]() dans
l'équation générale.
dans
l'équation générale.
Le champ ![]() peut s'écrire :
peut s'écrire :
![]()
et l'équation résolue : ![]()
La variable d'état est le potentiel scalaire magnétique total : ϕtot
(noté V1 dans Flux)
Le potentiel scalaire réduit par rapport à Hj (3D)
Le potentiel scalaire magnétique réduit par rapport à Hj, ϕ redHj,
est utilisé dans le cas où les sources de courant sont des sources non maillées. Ce cas
correspond à ![]() dans
l'équation générale avec Hj calculé de façon analytique par Biot et Savart
(cf. § Magnéto Statique : sources non maillées (spécificité 3D)
).
dans
l'équation générale avec Hj calculé de façon analytique par Biot et Savart
(cf. § Magnéto Statique : sources non maillées (spécificité 3D)
).
Le champ ![]() peut s'écrire :
peut s'écrire :
![]()
et l'équation résolue : ![]()
La variable d'état est le potentiel scalaire magnétique réduit par rapport à Hj : ϕredHj (noté V1R dans Flux 3D)
Le potentiel scalaire réduit par rapport à T0 (3D)
Le potentiel scalaire magnétique réduit par rapport à T0, ϕ redTo,
est utilisé dans le cas où les sources de courant sont des sources maillées. Ce cas
correspond à ![]() dans
l'équation générale avec
dans
l'équation générale avec ![]() défini par
défini par ![]() (où
(où
![]() est la densité de
courant des sources maillées).
est la densité de
courant des sources maillées).
Le champ ![]() peut s'écrire :
peut s'écrire :
![]()
et l'équation résolue : ![]()
Les variables d'état sont alors :
-
le potentiel scalaire magnétique réduit par rapport à T0 : ϕredTo
(noté également V1R dans Flux)
-
le potentiel vecteur électrique
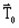
(non directement accessible dans Flux)