HyperKriging
Creates predictive models with data sets coming from deterministic computer simulations, an area of application commonly known as the Design and Analysis of Computer Experiments (DACE).
These experiments are unique because they do not require some concepts such as replication. This approximation method is designed to tightly pass through and smoothly interpolate between the known points.
Usability Characteristics
- Attempts to go through the exact sampling points, and in general, the residuals are small, if not zero. As a result, diagnostic measures using only the complete input matrix do not produce meaningful values. Cross-validation results provide some diagnostics using a special scheme using only the input points. To get detailed diagnostics on the quality of a HyperKriging Fit, it is suggested that you use a testing matrix.
- Suitable for modeling highly nonlinear output response data that does not contain numerical noise.
- Applicability of HyperKriging and Radial Basis Function methods are similar in terms of physics (they both are suggested for
highly nonlinear output responses with no noise). It is suggested that you
use HyperKriging for large studies that contain a large
number of sampling points, whereas, Radial Basis Function is
suggested for studies with a large number of variables. Note: As a result, Radial Basis Function Fits are evaluated faster than HyperKriging Fits when used in approaches.
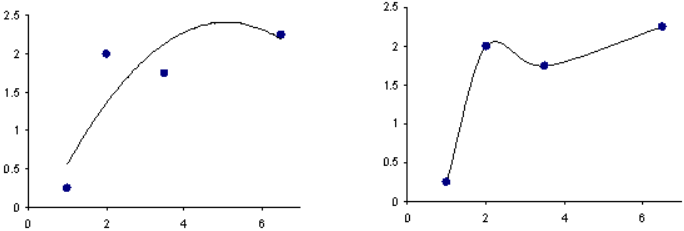
Figure 1. Comparison of a Quadratic Polynomial Model and aHyperKriging Model for a Function of a Single Variable. The plot on the left is a Least Squares Quadratic Regression, and the plot on the right is a HyperKriging model.
Settings
No settings available at this time.