Latin HyperCube
A square grid containing sample positions is a Latin square if, and only if, there is only one sample in each row and each column. A Latin HyperCube DOE, categorized as a space filling DOE, is the generalization of this concept to an arbitrary number of dimensions.
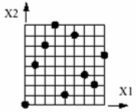
Figure 1.
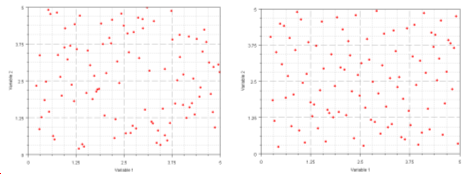
Figure 2. . Latin HyperCube (left) and Hammersley (right) for 100 runs.
Usability Characteristics
- To get a good quality fitting function, a minimum number of runs should be evaluated. (N+1)(N+2)/2 runs are needed to fit a second order polynomial, assuming that most output responses are close to a second order polynomial within the commonly used input variable ranges of -+10%. An additional number of runs equal to 10% is recommended to provide redundancy, which results in more reliable post-processing. As a result, this equation is recommend to calculate the number of runs needed or a minimum of 1.1*(N+1)(N+2)/2 runs.
- The structure of a Latin HyperCube run matrix ensures that the runs are orthogonal. Orthogonality is desirable because it is less likely to result in singularities when creating Least Squares Regression fits.
- Any data in the inclusion matrix is combined with the run data for post-processing. Any run matrix point which is already part of the inclusion data will not be rerun.
Settings
| Parameter | Default | Range | Description |
|---|---|---|---|
| Number of Runs | > 0 integer | Number of new designs to be evaluated. | |
| Random Seed | 1 | Integer 0 to 10000 |
Controlling repeatability of
runs depending on the way the sequence of random numbers is
generated.
|
| Use Inclusion Matrix | Off | Off or On | Concatenation without duplication between the inclusion and the generated run matrix. |