/BEM/FLOW
Block Format Keyword Describes the incompressible fluid flow by boundary elements method.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /BEM/FLOW/flow_ID/unit_ID | |||||||||
| flow_title | |||||||||
| surf_IDex | Nio | Iinside | fct_IDfsp | Fscalefsp | Ascalefsp | ||||
| grn_IDaux | Itest | Tole | |||||||
| Rho | Ivinf | ||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| surf_IDio | fct_IDnv | fct_IDp | Fscalenv | Fscalep | Ascalet | ||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| Iform | Ipri | Dtflow | |||||||
| fct_IDv | Fscalev | Ascalev | |||||||
| Dirx | Diry | Dirz | |||||||
Definitions
| Field | Contents | SI Unit Example |
|---|---|---|
| flow_ID | Incompressible flow block
identifier. (Integer, maximum 10 digits) |
|
| unit_ID | Unit Identifier. (Integer, maximum 10 digits) |
|
| flow_title | Incompressible flow block
title. (Character, maximum 100 characters) |
|
| surf_IDex | Flow external surface
identifier. (Integer) |
|
| Nio | Number of inflow-outflow
surfaces. (Integer) |
|
| Iinside | Inside or outside flow flag.
(Integer) |
|
| fct_IDfsp | Stagnation pressure curve
identifier. (Integer) |
|
| Fscalefsp | Stagnation pressure scale
factor. Default = 1.0 (Real) |
|
| Ascalefsp | Abcissa scale factor for
stagnation pressure curve. Default = 1.0 (Real) |
|
| grn_IDaux | Auxiliary nodes group
identifier. 2 (Integer) |
|
| Itest | Test auxiliary nodes flag.
2 (Integer > 0) |
|
| Tole | A dimensional tolerance.
2 Default = 1.e-5 (Real) |
|
| Rho | Fluid
density. (Real) |
|
| Ivinf | Additional velocity field
flag. 3 (Integer > 0) |
|
| surf_IDio | Inflow-Outflow surface
identifier. 4 (Integer) |
|
| fct_IDnv | Normal velocity curve.
4 (Integer) |
|
| fct_IDp | Imposed pressure curve.
5 (Integer) |
|
| Fscalenv | Normal velocity scale
factor. Default = 1.0 (Real) |
|
| Fscalep | Imposed pressure scale
factor. Default = 1.0 (Real) |
|
| Ascalet | Abscissa scale factor for
normal velocity curve and imposed pressure curve. Default = 1.0 (Real) |
|
| Iform | Formulation flag. 6
(Integer > 1) |
|
| Ipri | Output level. (Integer > 1) |
|
| Dtflow | Time step for BEM matrices
assembly. 7
(Real) |
|
| fct_IDv | Velocity curve
identifier. (Integer) |
|
| Fscalev | Velocity scale
factor. Default = 1.0 (Real) |
|
| Ascalev | Abscissa scale factor for
velocity curve. Default = 1.0 (Real) |
|
| Dirx | X component of the
additional field direction vector. (Real) |
|
| Diry | Y component of the
additional field direction vector. (Real) |
|
| Dirz | Z component of the
additional field direction vector. (Real) |
Example
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/BEM/FLOW/1
Flow 1
#surf_IDex Nio Iinside fct_IDfsp Fscale_fsp Ascale_fsp
3 2 1 0 0. 0.
#grn_IDaux Itest Tole
1 0 1e-5
# Rho Ivinf
1.0 0
#surf_IDio fct_IDnv fct_IDp Fscale_nv Fscale_p Ascale_t
2 1 0 10.0 0.0 1.0
#surf_IDio fct_IDnv fct_IDp Fscale_nv Fscale_p Ascale_t
1 0 1 0.0 101325.0 1.0
# Iform Ipri Dt_flow
1 1 1e-3
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/1
Function 1
# X Y
0 1
100 1
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#enddata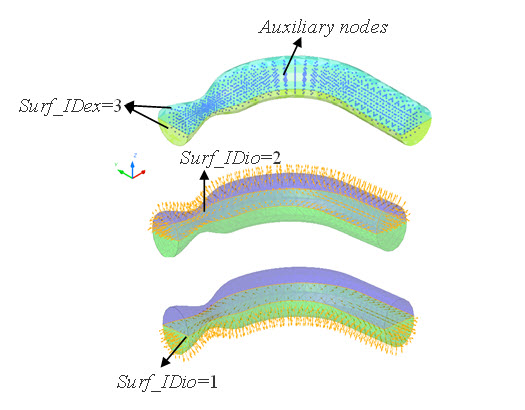
Figure 1.
Comments
- The surf_IDex must define a closed surface.
- Using BEM, the flow
potential, velocity and pressure are computed for nodes belonging to the surface
defined by surf_IDex.
For visual and post-treatment concerns, the flow characteristics can be computed for a set of nodes inside the flow belonging to grn_IDaux.
If Itest = 1, whether the auxiliary nodes are actually located inside (if Iinside =1) or outside (if Iinside =2), the surface defined by surf_IDex at each time step is tested. Inorrect nodes are then canceled for the current time step.
Tolerance Tole is used to perform the point-inside-closed-surface test.
- Flag
Ivinf is only effective
for flow computation in an unbounded domain outside the surface defined by
surf_IDex
(Iinside
=2).
If Ivinf = 1, an inflow condition is defined by an additional homogeneous flow defined in free space. The computed flow will be identical to the additional flow at an infinite distance from the surface defined by surf_IDex.
- If
Iinside =
0: Flow is computed inside the surface defined by
surf_IDex. There must be at
least one surface where the normal velocity is imposed and only one surface
where the normal velocity could be left as free. The velocity at the free
surface will be computed thanks to flux equilibrium on the global surface
defined by surf_IDex.
If Iinside = 2 and Ivinf = 0: Iinside = 0 but flow is computed outside the surface defined by surf_IDex.
If Iinside = 2 and Ivinf = 1: numbers of surface could be free and the normal velocity must be imposed on all of them.
- In order to reduce pressure from the velocity field, one and only one pressure must be imposed for the entire flow computation: it can be either the global stagnation pressure or the pressure at one of the inflow-outflow surfaces.
- The collocation approach is
faster but may not be robust enough to handle very complex geometries.
The Galerkin approach works in every situation but is significantly slower.
- BEM matrices depend only on
the geometry of the surface.
If Dtflow = 0 (default), they are assembled at every cycle of the simulation (the time step being classically given by the stability condition of finite elements).
If Dtflow ≠ 0: max(Dtflow, Dt) is used to update to BEM matrices; where Dt is the finite element time step.