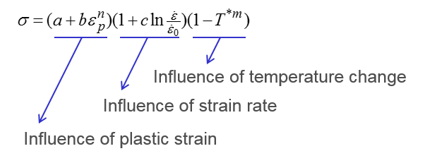
In Radioss material laws LAW32, LAW43, LAW72, LAW73,
LAW74, LAW78 and LAW93 use HILL criteria.
HILL Criteria
The typical HILL criteria is:
3D equivalent HILL stress:(6)
f =
F
(
σ
y y
−
σ
z z
)
2
+ G
(
σ
z z
−
σ
x x
)
2
+ H
(
σ
x x
−
σ
y y
)
2
+ 2 L
σ
y z
2
+ 2 M
σ
z x
2
+ 2 N
σ
x y
2
=
(
G + H
)
︸
σ
x x
2
+
(
F + H
)
︸
σ
y y
2
+
(
F + G
)
︸
σ
z z
2
−
2 H
︸
σ
x x
σ
y y
−
2 F
︸
σ
y y
σ
z z
−
2 G
︸
σ
z z
σ
x x
+
2 L
︸
σ
y z
2
+
2 M
︸
σ
z x
2
+
2 N
︸
σ
x y
2
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakqaabeqaaiaadA
gacqGH9aqpdaGcaaqaaiaadAeadaqadiqaaiabeo8aZnaaBaaaleaa
caWG5bGaamyEaaqabaGccqGHsislcqaHdpWCdaWgaaWcbaGaamOEai
aadQhaaeqaaaGccaGLOaGaayzkaaWaaWbaaSqabeaacaaIYaaaaOGa
ey4kaSIaam4ramaabmGabaGaeq4Wdm3aaSbaaSqaaiaadQhacaWG6b
aabeaakiabgkHiTiabeo8aZnaaBaaaleaacaWG4bGaamiEaaqabaaa
kiaawIcacaGLPaaadaahaaWcbeqaaiaaikdaaaGccqGHRaWkcaWGib
WaaeWaceaacqaHdpWCdaWgaaWcbaGaamiEaiaadIhaaeqaaOGaeyOe
I0Iaeq4Wdm3aaSbaaSqaaiaadMhacaWG5baabeaaaOGaayjkaiaawM
caamaaCaaaleqabaGaaGOmaaaakiabgUcaRiaaygW7caaIYaGaamit
aiabeo8aZnaaDaaaleaacaWG5bGaamOEaaqaaiaaikdaaaGccqGHRa
WkcaaIYaGaamytaiabeo8aZnaaDaaaleaacaWG6bGaamiEaaqaaiaa
ikdaaaGccqGHRaWkcaaIYaGaamOtaiabeo8aZnaaDaaaleaacaWG4b
GaamyEaaqaaiaaikdaaaaabeaaaOqaaiaabccacaqGGaGaaeiiaiaa
b2dadaGcaaqaamaayaaabaWaaeWaaeaacaWGhbGaey4kaSIaamisaa
GaayjkaiaawMcaaaWcbaaakiaawIJ=aiabeo8aZnaaDaaaleaacaWG
4bGaamiEaaqaaiaaikdaaaGccqGHRaWkdaagaaqaamaabmaabaGaam
OraiabgUcaRiaadIeaaiaawIcacaGLPaaaaSqaaaGccaGL44pacqaH
dpWCdaqhaaWcbaGaamyEaiaadMhaaeaacaaIYaaaaOGaey4kaSYaaG
baaeaadaqadaqaaiaadAeacqGHRaWkcaWGhbaacaGLOaGaayzkaaaa
leaaaOGaayjo+dGaeq4Wdm3aa0baaSqaaiaadQhacaWG6baabaGaaG
OmaaaakiabgkHiTmaayaaabaGaaGOmaiaadIeaaSqaaaGccaGL44pa
cqaHdpWCdaWgaaWcbaGaamiEaiaadIhaaeqaaOGaeq4Wdm3aaSbaaS
qaaiaadMhacaWG5baabeaakiabgkHiTmaayaaabaGaaGOmaiaadAea
aSqaaaGccaGL44pacqaHdpWCdaWgaaWcbaGaamyEaiaadMhaaeqaaO
Gaeq4Wdm3aaSbaaSqaaiaadQhacaWG6baabeaakiabgkHiTmaayaaa
baGaaGOmaiaadEeaaSqaaaGccaGL44pacqaHdpWCdaWgaaWcbaGaam
OEaiaadQhaaeqaaOGaeq4Wdm3aaSbaaSqaaiaadIhacaWG4baabeaa
kiabgUcaRmaayaaabaGaaGzaVlaaikdacaWGmbaaleaaaOGaayjo+d
Gaeq4Wdm3aa0baaSqaaiaadMhacaWG6baabaGaaGOmaaaakiabgUca
RmaayaaabaGaaGOmaiaad2eaaSqaaaGccaGL44pacqaHdpWCdaqhaa
WcbaGaamOEaiaadIhaaeaacaaIYaaaaOGaey4kaSYaaGbaaeaacaaI
YaGaamOtaaWcbaaakiaawIJ=aiabeo8aZnaaDaaaleaacaWG4bGaam
yEaaqaaiaaikdaaaaabeaaaaaa@DD25@
Shell element:(7)
f
=
F
σ
y
y
2
+
G
σ
x
x
2
+
H
(
σ
x
x
−
σ
y
y
)
2
+
2
N
σ
x
y
2
=
(
G
+
H
)
︸
σ
x
x
2
+
(
F
+
H
)
︸
σ
y
y
2
−
2
H
︸
σ
x
x
σ
y
y
+
2
N
︸
σ
x
y
2
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGMbGaey
ypa0ZaaOaaaeaacaWGgbGaeq4Wdm3aa0baaSqaaiaadMhacaWG5baa
baGaaGOmaaaakiabgUcaRiaadEeacqaHdpWCdaqhaaWcbaGaamiEai
aadIhaaeaacaaIYaaaaOGaey4kaSIaamisamaabmGabaGaeq4Wdm3a
aSbaaSqaaiaadIhacaWG4baabeaakiabgkHiTiabeo8aZnaaBaaale
aacaWG5bGaamyEaaqabaaakiaawIcacaGLPaaadaahaaWcbeqaaiaa
ikdaaaGccqGHRaWkcaaIYaGaamOtaiabeo8aZnaaDaaaleaacaWG4b
GaamyEaaqaaiaaikdaaaaabeaakiabg2da9maakaaabaWaaGbaaeaa
daqadaqaaiaadEeacqGHRaWkcaWGibaacaGLOaGaayzkaaaaleaaaO
Gaayjo+dGaeq4Wdm3aa0baaSqaaiaadIhacaWG4baabaGaaGOmaaaa
kiabgUcaRmaayaaabaWaaeWaaeaacaWGgbGaey4kaSIaamisaaGaay
jkaiaawMcaaaWcbaaakiaawIJ=aiabeo8aZnaaDaaaleaacaWG5bGa
amyEaaqaaiaaikdaaaGccqGHsisldaagaaqaaiaaikdacaWGibaale
aaaOGaayjo+dGaeq4Wdm3aaSbaaSqaaiaadIhacaWG4baabeaakiab
eo8aZnaaBaaaleaacaWG5bGaamyEaaqabaGccqGHRaWkdaagaaqaai
aaikdacaWGobaaleaaaOGaayjo+dGaeq4Wdm3aa0baaSqaaiaadIha
caWG5baabaGaaGOmaaaaaeqaaaaa@863E@
Where,
F
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOraaaa@36C1@
G
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOraaaa@36C1@
H
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOraaaa@36C1@
L
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOraaaa@36C1@
M
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOraaaa@36C1@
N
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOraaaa@36C1@
F
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOraaaa@36C1@
G
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOraaaa@36C1@
H
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOraaaa@36C1@
N
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOraaaa@36C1@
In LAW78, the HILL criteria is:
(8)
φ
(
A
)
=
1
︸
G
+
H
⋅
A
x
x
2
−
2
r
0
1
+
r
0
︸
2
H
A
x
x
A
y
y
+
r
0
(
1
+
r
90
)
r
90
(
1
+
r
0
)
︸
F
+
H
A
y
y
2
+
r
0
+
r
90
r
90
(
1
+
r
0
)
(
2
r
45
+
1
)
︸
2
N
A
x
y
2
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacqaHgpGAca
GGOaGaamyqaiaacMcacqGH9aqpdaagaaqaaiaaigdaaSqaaiaadEea
cqGHRaWkcaWGibaakiaawIJ=aiabgwSixlaadgeadaqhaaWcbaGaam
iEaiaadIhaaeaacaaIYaaaaOGaeyOeI0YaaGbaaeaadaWcaaqaaiaa
ikdacaWGYbWaaSbaaSqaaiaaicdaaeqaaaGcbaGaaGymaiabgUcaRi
aadkhadaWgaaWcbaGaaGimaaqabaaaaaqaaiaaikdacaWGibaakiaa
wIJ=aiaadgeadaWgaaWcbaGaamiEaiaadIhaaeqaaOGaamyqamaaBa
aaleaacaWG5bGaamyEaaqabaGccqGHRaWkdaagaaqaamaalaaabaGa
amOCamaaBaaaleaacaaIWaaabeaakmaabmaabaGaaGymaiabgUcaRi
aadkhadaWgaaWcbaGaaGyoaiaaicdaaeqaaaGccaGLOaGaayzkaaaa
baGaamOCamaaBaaaleaacaaI5aGaaGimaaqabaGcdaqadaqaaiaaig
dacqGHRaWkcaWGYbWaaSbaaSqaaiaaicdaaeqaaaGccaGLOaGaayzk
aaaaaaWcbaGaamOraiabgUcaRiaadIeaaOGaayjo+dGaamyqamaaDa
aaleaacaWG5bGaamyEaaqaaiaaikdaaaGccqGHRaWkdaagaaqaamaa
laaabaGaamOCamaaBaaaleaacaaIWaaabeaakiabgUcaRiaadkhada
WgaaWcbaGaaGyoaiaaicdaaeqaaaGcbaGaamOCamaaBaaaleaacaaI
5aGaaGimaaqabaGcdaqadaqaaiaaigdacqGHRaWkcaWGYbWaaSbaaS
qaaiaaicdaaeqaaaGccaGLOaGaayzkaaaaamaabmaabaGaaGOmaiaa
dkhadaWgaaWcbaGaaGinaiaaiwdaaeqaaOGaey4kaSIaaGymaaGaay
jkaiaawMcaaaWcbaGaaGOmaiaad6eaaOGaayjo+dGaamyqamaaDaaa
leaacaWG4bGaamyEaaqaaiaaikdaaaaaaa@8B69@
There are two ways to determine HILL parameters
by using Lankford parameters.
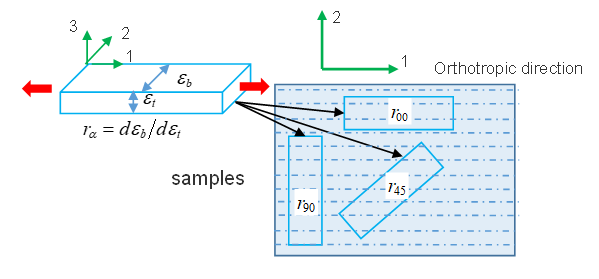
Strain ratio
r
00
,
r
45
,
r
90
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOCamaaBa
aaleaacaaIWaGaaGimaaqabaGccaGGSaGaamOCamaaBaaaleaacaaI
0aGaaGynaaqabaGccaGGSaGaamOCamaaBaaaleaacaaI5aGaaGimaa
qabaaaaa@3F42@
Yield stress ratio
R
11
,
R
22
,
R
33
,
R
12
,
R
13
,
R
23
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOuamaaBa
aaleaacaaIXaGaaGymaaqabaGccaGGSaGaamOuamaaBaaaleaacaaI
YaGaaGOmaaqabaGccaGGSaGaamOuamaaBaaaleaacaaIZaGaaG4maa
qabaGccaGGSaGaamOuamaaBaaaleaacaaIXaGaaGOmaaqabaGccaGG
SaGaamOuamaaBaaaleaacaaIXaGaaG4maaqabaGccaGGSaGaamOuam
aaBaaaleaacaaIYaGaaG4maaqabaaaaa@487B@
Strain Ratio
The Lankford parameters
r
α
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaqaaaaaaaaa
WdbiaadkhapaWaaSbaaSqaa8qacqaHXoqya8aabeaaaaa@396F@
is the ratio of plastic strain in plane and plastic
strain in thickness direction
ε
33
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaqaaaaaaaaa
Wdbiabew7aL9aadaWgaaWcbaWdbiaaiodacaaIZaaapaqabaaaaa@39FA@
.
(9)
r
α
=
d
ε
α
+
π
/
2
d
ε
33
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaqaaaaaaaaa
WdbiaadkhapaWaaSbaaSqaa8qacqaHXoqya8aabeaak8qacqGH9aqp
daWcaaWdaeaapeGaamizaiabew7aL9aadaWgaaWcbaWdbiabeg7aHj
abgUcaRiabec8aWjaac+cacaaIYaaapaqabaaakeaapeGaamizaiab
ew7aL9aadaWgaaWcbaWdbiaaiodacaaIZaaapaqabaaaaaaa@47D3@
Where,
α
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaaleaaqaaaaaaaaa
Wdbiabeg7aHbaa@381F@
r
α
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaqaaaaaaaaa
WdbiaadkhapaWaaSbaaSqaa8qacqaHXoqya8aabeaaaaa@396F@
r
00
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOCamaaBa
aaleaacaaIWaGaaGimaaqabaaaaa@388E@
r
90
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOCamaaBa
aaleaacaaI5aGaaGimaaqabaaaaa@3897@
The strain ratio is the strain in width direction of sample to strain in thickness
direction of sample.
Figure 10.
In this case, the HILL parameters are:
(10)
F
=
r
00
r
90
(
r
00
+
1
)
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGgbGaey
ypa0ZaaSaaaeaacaWGYbWaaSbaaSqaaiaaicdacaaIWaaabeaaaOqa
aiaadkhadaWgaaWcbaGaaGyoaiaaicdaaeqaaOGaaiikaiaadkhada
WgaaWcbaGaaGimaiaaicdaaeqaaOGaey4kaSIaaGymaiaacMcaaaaa aa@4322@
(11)
G
=
1
(
r
00
+
1
)
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGhbGaey
ypa0ZaaSaaaeaacaaIXaaabaGaaiikaiaadkhadaWgaaWcbaGaaGim
aiaaicdaaeqaaOGaey4kaSIaaGymaiaacMcaaaaaaa@3E93@
(12)
H
=
r
00
(
r
00
+
1
)
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGibGaey
ypa0ZaaSaaaeaacaWGYbWaaSbaaSqaaiaaicdacaaIWaaabeaaaOqa
aiaacIcacaWGYbWaaSbaaSqaaiaaicdacaaIWaaabeaakiabgUcaRi
aaigdacaGGPaaaaaaa@407A@
(13)
N
=
(
1
+
2
r
45
)
(
r
00
+
r
90
)
2
r
90
(
r
00
+
1
)
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGobGaey
ypa0ZaaSaaaeaacaGGOaGaaGymaiabgUcaRiaaikdacaWGYbWaaSba
aSqaaiaaisdacaaI1aaabeaakiaacMcacaGGOaGaamOCamaaBaaale
aacaaIWaGaaGimaaqabaGccqGHRaWkcaWGYbWaaSbaaSqaaiaaiMda
caaIWaaabeaakiaacMcaaeaacaaIYaGaamOCamaaBaaaleaacaaI5a
GaaGimaaqabaGccaGGOaGaamOCamaaBaaaleaacaaIWaGaaGimaaqa
baGccqGHRaWkcaaIXaGaaiykaaaaaaa@4F27@
Here,
G
+
H
=
1
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGhbGaey
4kaSIaamisaiabg2da9iaaigdaaaa@3A9B@
In LAW32, LAW43, and LAW73, the HILL criteria is:
(14)
σ
e
q
=
A
1
σ
1
2
+
A
2
σ
2
2
−
A
3
σ
1
σ
2
+
A
12
σ
12
2
R
=
r
00
+
2
r
45
+
r
90
4
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGsbGaey
ypa0ZaaSaaaeaacaWGYbWaaSbaaSqaaiaaicdacaaIWaaabeaakiab
gUcaRiaaikdacaWGYbWaaSbaaSqaaiaaisdacaaI1aaabeaakiabgU
caRiaadkhadaWgaaWcbaGaaGyoaiaaicdaaeqaaaGcbaGaaGinaaaa
aaa@437F@
H
=
R
1
+
R
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGibGaey
ypa0ZaaSaaaeaacaWGsbaabaGaaGymaiabgUcaRiaadkfaaaaaaa@3B8D@
A
1
=
H
(
1
+
1
r
00
)
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGbbWaaS
baaSqaaiaaigdaaeqaaOGaeyypa0JaamisamaabmaabaGaaGymaiab
gUcaRmaalaaabaGaaGymaaqaaiaadkhadaWgaaWcbaGaaGimaiaaic
daaeqaaaaaaOGaayjkaiaawMcaaaaa@407B@
A
2
=
H
(
1
+
1
r
90
)
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGbbWaaS
baaSqaaiaaikdaaeqaaOGaeyypa0JaamisamaabmaabaGaaGymaiab
gUcaRmaalaaabaGaaGymaaqaaiaadkhadaWgaaWcbaGaaGyoaiaaic
daaeqaaaaaaOGaayjkaiaawMcaaaaa@4085@
A
3
=
2
H
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGbbWaaS
baaSqaaiaaiodaaeqaaOGaeyypa0JaaGOmaiaadIeaaaa@3AA7@
A
12
=
2
H
(
r
45
+
0.5
)
(
1
r
00
+
1
r
90
)
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGbbWaaS
baaSqaaiaaigdacaaIYaaabeaakiabg2da9iaaikdacaWGibGaaiik
aiaadkhadaWgaaWcbaGaaGinaiaaiwdaaeqaaOGaey4kaSIaaGimai
aac6cacaaI1aGaaiykamaabmaabaWaaSaaaeaacaaIXaaabaGaamOC
amaaBaaaleaacaaIWaGaaGimaaqabaaaaOGaey4kaSYaaSaaaeaaca
aIXaaabaGaamOCamaaBaaaleaacaaI5aGaaGimaaqabaaaaaGccaGL
OaGaayzkaaaaaa@4BBD@
They all request Lankford parameter (strain ratio)
r
00
,
r
45
,
r
90
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOCamaaBa
aaleaacaaIWaGaaGimaaqabaGccaGGSaGaamOCamaaBaaaleaacaaI
0aGaaGynaaqabaGccaGGSaGaamOCamaaBaaaleaacaaI5aGaaGimaa
qabaaaaa@3F42@
A
i
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqamaaBa
aaleaacaWGPbaabeaaaaa@37D6@
Radioss .
Yield Stress Ratio
In LAW93, the yield stress ratio used is:
(15)
R
i
j
=
σ
i
j
σ
0
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOuamaaBa
aaleaacaWGPbGaamOAaaqabaGccqGH9aqpdaWcaaqaaiabeo8aZnaa
BaaaleaacaWGPbGaamOAaaqabaaakeaacqaHdpWCdaWgaaWcbaGaaG
imaaqabaaaaaaa@4076@
To get yield stress ratio
R
i
j
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOuamaaBa
aaleaacaWGPbGaamOAaaqabaaaaa@38D7@
, yield stress in two loading cases need to be
measured.
Yield stress
σ
11
,
σ
22
,
σ
33
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdm3aaS
baaSqaaiaaigdacaaIXaaabeaakiaacYcacqaHdpWCdaWgaaWcbaGa
aGOmaiaaikdaaeqaaOGaaiilaiabeo8aZnaaBaaaleaacaaIZaGaaG
4maaqabaaaaa@41A0@
Yield shear stress
σ
12
,
σ
13
,
σ
23
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdm3aaS
baaSqaaiaaigdacaaIYaaabeaakiaacYcacqaHdpWCdaWgaaWcbaGa
aGymaiaaiodaaeqaaOGaaiilaiabeo8aZnaaBaaaleaacaaIYaGaaG
4maaqabaaaaa@41A0@
In LAW93, if parameter input is used, then take initial stress parameter
σ
y
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdm3aaS
baaSqaaiaadMhaaeqaaaaa@38E4@
σ
0
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdm3aaS
baaSqaaiaaicdaaeqaaaaa@38A0@
σ
0
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdm3aaS
baaSqaaiaaicdaaeqaaaaa@38A0@
Four HILL parameters for shell are automatically computed by
Radioss .
(16)
F
=
1
2
(
1
R
22
2
+
1
R
33
2
−
1
R
11
2
)
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOraiabg2
da9maalaaabaGaaGymaaqaaiaaikdaaaGaaiikamaalaaabaGaaGym
aaqaaiaadkfadaqhaaWcbaGaaGOmaiaaikdaaeaacaaIYaaaaaaaki
abgUcaRmaalaaabaGaaGymaaqaaiaadkfadaqhaaWcbaGaaG4maiaa
iodaaeaacaaIYaaaaaaakiabgkHiTmaalaaabaGaaGymaaqaaiaadk
fadaqhaaWcbaGaaGymaiaaigdaaeaacaaIYaaaaaaakiaacMcaaaa@489E@
(17)
G
=
1
2
(
1
R
33
2
+
1
R
11
2
−
1
R
22
2
)
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4raiabg2
da9maalaaabaGaaGymaaqaaiaaikdaaaGaaiikamaalaaabaGaaGym
aaqaaiaadkfadaqhaaWcbaGaaG4maiaaiodaaeaacaaIYaaaaaaaki
abgUcaRmaalaaabaGaaGymaaqaaiaadkfadaqhaaWcbaGaaGymaiaa
igdaaeaacaaIYaaaaaaakiabgkHiTmaalaaabaGaaGymaaqaaiaadk
fadaqhaaWcbaGaaGOmaiaaikdaaeaacaaIYaaaaaaakiaacMcaaaa@489F@
(18)
H
=
1
2
(
1
R
22
2
+
1
R
11
2
−
1
R
33
2
)
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamisaiabg2
da9maalaaabaGaaGymaaqaaiaaikdaaaGaaiikamaalaaabaGaaGym
aaqaaiaadkfadaqhaaWcbaGaaGOmaiaaikdaaeaacaaIYaaaaaaaki
abgUcaRmaalaaabaGaaGymaaqaaiaadkfadaqhaaWcbaGaaGymaiaa
igdaaeaacaaIYaaaaaaakiabgkHiTmaalaaabaGaaGymaaqaaiaadk
fadaqhaaWcbaGaaG4maiaaiodaaeaacaaIYaaaaaaakiaacMcaaaa@48A0@
(19)
N
=
3
2
R
12
2
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOtaiabg2
da9maalaaabaGaaG4maaqaaiaaikdacaWGsbWaa0baaSqaaiaaigda
caaIYaaabaGaaGOmaaaaaaaaaa@3C90@
In LAW74, yield stress ratio
R
i
j
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOuamaaBa
aaleaacaWGPbGaamOAaaqabaaaaa@38D7@
is used with yield stress
σ
11
,
σ
22
,
σ
33
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdm3aaS
baaSqaaiaaigdacaaIXaaabeaakiaacYcacqaHdpWCdaWgaaWcbaGa
aGOmaiaaikdaaeqaaOGaaiilaiabeo8aZnaaBaaaleaacaaIZaGaaG
4maaqabaaaaa@41A0@
and
σ
12
,
σ
13
,
σ
23
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdm3aaS
baaSqaaiaaigdacaaIYaaabeaakiaacYcacqaHdpWCdaWgaaWcbaGa
aGymaiaaiodaaeqaaOGaaiilaiabeo8aZnaaBaaaleaacaaIYaGaaG
4maaqabaaaaa@41A0@
input directly, and then six HILL parameters for
solid are automatically computed by
Radioss .
F
=
1
2
(
1
σ
22
2
+
1
σ
33
2
−
1
σ
11
2
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGgbGaey
ypa0ZaaSaaaeaacaaIXaaabaGaaGOmaaaadaqadaqaamaalaaabaGa
aGymaaqaaiabeo8aZnaaDaaaleaacaaIYaGaaGOmaaqaaiaaikdaaa
aaaOGaey4kaSYaaSaaaeaacaaIXaaabaGaeq4Wdm3aa0baaSqaaiaa
iodacaaIZaaabaGaaGOmaaaaaaGccqGHsisldaWcaaqaaiaaigdaae
aacqaHdpWCdaqhaaWcbaGaaGymaiaaigdaaeaacaaIYaaaaaaaaOGa
ayjkaiaawMcaaaaa@4BF9@
G
=
1
2
(
1
σ
22
2
+
1
σ
33
2
−
1
σ
11
2
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGhbGaey
ypa0ZaaSaaaeaacaaIXaaabaGaaGOmaaaadaqadaqaamaalaaabaGa
aGymaaqaaiabeo8aZnaaDaaaleaacaaIYaGaaGOmaaqaaiaaikdaaa
aaaOGaey4kaSYaaSaaaeaacaaIXaaabaGaeq4Wdm3aa0baaSqaaiaa
iodacaaIZaaabaGaaGOmaaaaaaGccqGHsisldaWcaaqaaiaaigdaae
aacqaHdpWCdaqhaaWcbaGaaGymaiaaigdaaeaacaaIYaaaaaaaaOGa
ayjkaiaawMcaaaaa@4BFA@
H
=
1
2
(
1
σ
22
2
+
1
σ
33
2
−
1
σ
11
2
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGibGaey
ypa0ZaaSaaaeaacaaIXaaabaGaaGOmaaaadaqadaqaamaalaaabaGa
aGymaaqaaiabeo8aZnaaDaaaleaacaaIYaGaaGOmaaqaaiaaikdaaa
aaaOGaey4kaSYaaSaaaeaacaaIXaaabaGaeq4Wdm3aa0baaSqaaiaa
iodacaaIZaaabaGaaGOmaaaaaaGccqGHsisldaWcaaqaaiaaigdaae
aacqaHdpWCdaqhaaWcbaGaaGymaiaaigdaaeaacaaIYaaaaaaaaOGa
ayjkaiaawMcaaaaa@4BFB@
L
=
1
2
σ
23
2
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGmbGaey
ypa0ZaaSaaaeaacaaIXaaabaGaaGOmaiabeo8aZnaaDaaaleaacaaI
YaGaaG4maaqaaiaaikdaaaaaaaaa@3DE1@
M
=
1
2
σ
31
2
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGnbGaey
ypa0ZaaSaaaeaacaaIXaaabaGaaGOmaiabeo8aZnaaDaaaleaacaaI
ZaGaaGymaaqaaiaaikdaaaaaaaaa@3DE1@
N
=
1
2
σ
12
2
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGobGaey
ypa0ZaaSaaaeaacaaIXaaabaGaaGOmaiabeo8aZnaaDaaaleaacaaI
XaGaaGOmaaqaaiaaikdaaaaaaaaa@3DE1@
For shell element, take
M
=
N
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGnbGaey
ypa0JaamOtaaaa@3909@
L
=
N
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGnbGaey
ypa0JaamOtaaaa@3909@