Tabulated Failure Model /FAIL/TAB1

The stress state at a point, P, could be expressed with principle stresses (${\sigma }_1,{\sigma }_2,{\sigma }_3$) or could also be expressed using stress invariants ($I_1,J_2,J_3$). The advantage of using stress invariants is that they are constant and do not depend on the orientation of the coordinate system. In Figure 2, to correctly describe stress state of point P ${\sigma }_1,{\sigma }_2,{\sigma }_3$ using stress invariants, the magnitude of $OO\text{'}$ as:(1) $\sqrt{3}{\sigma }_m=\frac{\sqrt{3}}{3}{I}_1$

Where,

${\sigma }_m$

Mean stress

$I_1$

First stress invariant $I_1={\text{σ}}_1+{\text{σ}}_2+{\text{σ}}_3$

$OO\text{'}$ is in the hydrostatic axis, which means the principle stress in this axis is the same (${\sigma }_1={\sigma }_2={\sigma }_3$). $\left|OO\text{'}\right|$ is the hydrostatic pressure.

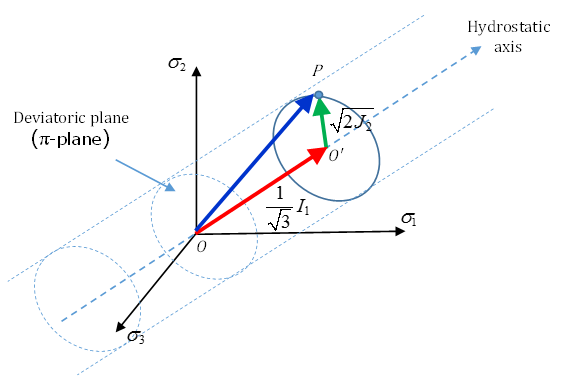
Figure 2. Stress State of P

The magnitude of $O\text{'}P$ is:(2) $$\sqrt{2J_2}=\sqrt{\frac{2}{3}}{\sigma }_{VM}$$

To identify the point P, the angle in the circular plane must be calculated. This angle is called the Lode Angle $\theta$:(3) $\text{cos}\left(3\theta \right)=\frac{27}{2}\frac{J_3}{{\sigma }_{VM}^3}=\frac{3\sqrt{3}}{2}\frac{J_3}{J_2^{3/2}}$

with $0\le \theta \le \frac{\pi }{3}$ and $J_3$ is the third invariant of deviatoric stress calculated as:(4) $J_3={\text{S}}_1{\text{S}}_2{\text{S}}_3$

In /FAIL/TAB1 a normalized and dimensionless Lode Angle parameter $\xi$ with the range $\left(-1\le \xi \le 1\right)$ is used and defined as:(5) $\xi =\text{cos}\left(3\theta \right)$

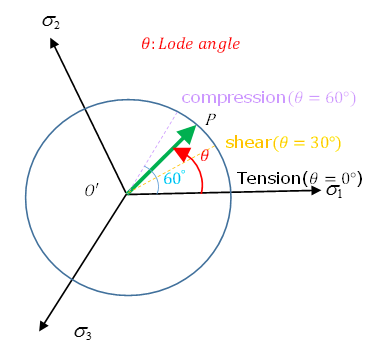
Figure 3. Stress State with Different Lode Angle

The special characters for Lode Angle $\theta$ and Load Angle Parameter $\xi$ are:

A failure strain surface can be created from the stress triaxiality and Lode angle failure data.

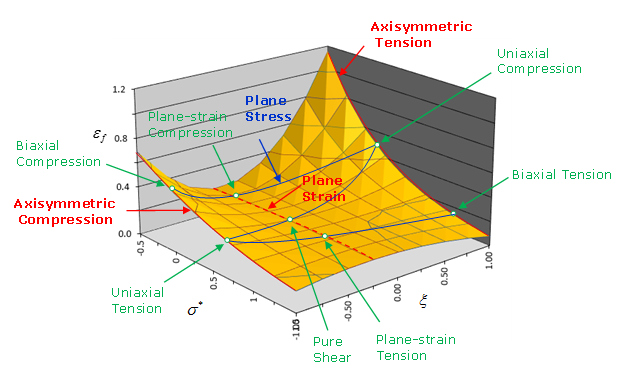
Figure 4. 3D Failure Surface

The material failure surface could be created using the following material tests.

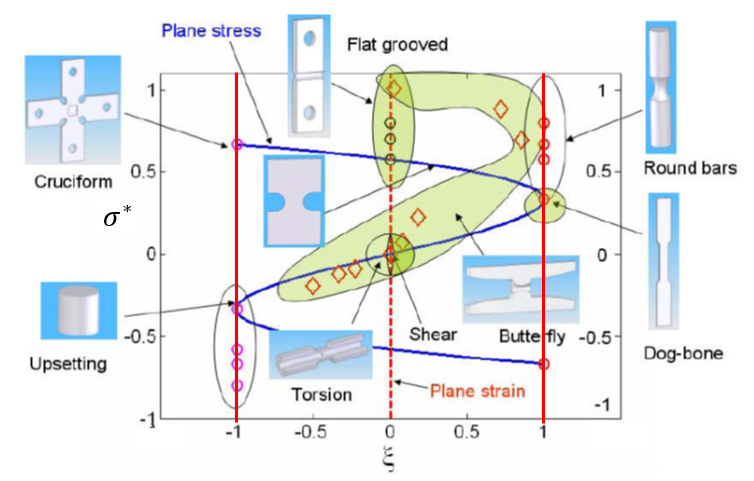
Figure 5. Stress State and Lode Angle for Various Tests

Input for failure plastic-strain versus triaxiality, strain rate, and Lode angle using table_ID₁

/TABLE/1/4711
failure plastic-strain vs triaxiality and strain rate
#dimension
         3
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#   FCT_ID                   strain_rate          Lode_angle  
      3000                          1E-4                  -1
      3001                           0.1                   0
      3002                           1.0                   1
....

Figure 6. Failure Surface when table_ID₁ references a /TABLE with dimension=3

Material failure based on temperature and element size can be considering in /FAIL/TAB1 by including functions that scale the failure strain depending on the element size and/or temperature using:(6) $${\epsilon }_f=Xscale1\cdot f({\sigma }^{*},\dot{\epsilon },\xi )\cdot facto{r}_{el}\cdot facto{r}_T$$

Where,

$$Xscale1$$

General scaling factor

$$facto{r}_{el}$$

Scale factor based on element size

$$facto{r}_T$$

Scale factor based on temperature

In numerical simulations, the element size will affect the material failure. Using the same failure parameters, a coarse mesh will fail earlier than a fine mesh.

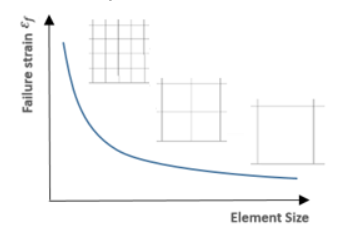
Figure 7. Influence of Element Mesh Size on Material Failure in Numerical Simulation

To account for the variation in results based on mesh size, the element size scale factor can be defined to scale the failure strain based on mesh element size. The scale factor defined in Equation 6 is:(7) $$facto{r}_{el}=Fscal{e}_{el}\cdot {\mathrm{f}}_{el}\left(\frac{Siz{e}_{el}}{El\_ref}\right)$$

Where,

$$Fscal{e}_{el}$$

Element size function scale factor

$${\mathrm{f}}_{el}\left(\frac{Siz{e}_{el}}{El\_ref}\right)$$

failure strain scale factor as a function of the normalized element size (defined via fct_ID_el), and $$El\_ref$$ is the reference element size used to normalize the element size

For example, a mesh size of 2mm was used in a material validation simulation. After the initial validation, the same simulation is reran using $$El\_ref$$ =2 with different element sizes to determine the correct scaling factor for each element size. Using the results of the second validation, a failure strain scale factor function is constructed as (Figure 8):

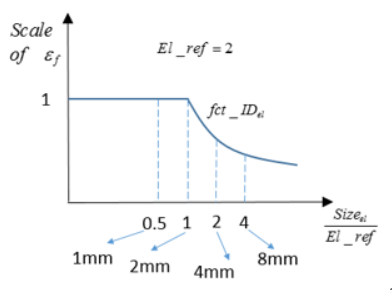
Figure 8. Example of Element Size Scale Factor Function fct_ID_el in /FAIL/TAB1

To account for how the temperature affects material failure, failure strain values defined in Equation 6 can be scaled using a temperature scale factor function:(8) $$facto{r}_T=Fscal{e}_T\cdot {\mathrm{f}}_T\left(T_{start}\right)$$

Where,

$$Fscal{e}_T$$

Temperature function scale factor

$${\mathrm{f}}_T\left(T_{start}\right)$$

Failure strain scale factor as a function temperature defined via fct_ID_T.

In fct_ID_T, the temperature is defined relative to the melting and initial temperature.(9) $$T^{\ast }=\frac{T-T_{ini}}{T_{melt}-T_{ini}}$$

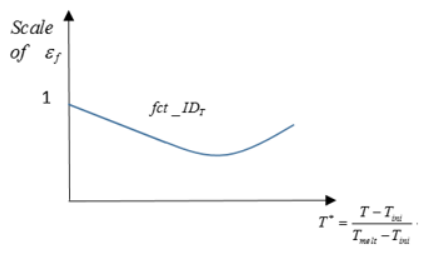
Figure 9. Influence of Temperature on Material Failure with fct_ID_T in /FAIL/TAB1

The accumulated damage is calculated by first calculating a damage increment:(10) $$\text{Δ}D=\frac{\text{Δ}{\epsilon }_p}{{\epsilon }_f}\cdot n\cdot D_p{}^{\left(1-\frac{1}{n}\right)}$$

Where,

$$\text{Δ}{\epsilon }_p$$

The change in plastic strain of the integration point

$${\epsilon }_f$$

Plastic failure strain for the current stress triaxiality

$$D_p$$ and $$n$$

Damage parameters

The accumulated damage is:(11) $D=\frac{{\displaystyle \sum \text{Δ}D}}{D_{crit}}$

Where, $D_{crit}$ is defined in /FAIL/TAB1 with a recommended between 0 and 1. The elements fail when $D\ge 1$ which means ${\displaystyle \sum \text{Δ}D}\ge D_{crit}$.

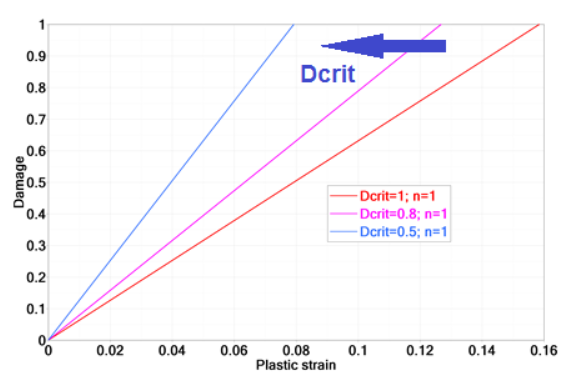
Figure 10. Influence of $D_{crit}$ in /FAIL/TAB1

When $$n$$=1 damage is linear, otherwise the damage curve is nonlinear.

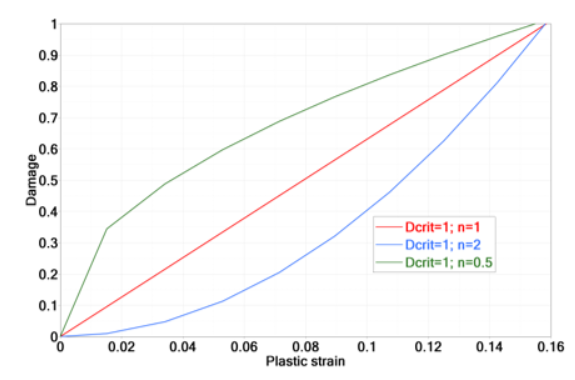
Figure 11. Influence of Damage Parameter $$n$$

In a tensile test, a material will reach a maximum engineering stress and then the stress will decrease or sometimes called soften. This maximum engineering stress point is called the necking point. After necking, the true stress actually increases, due to the decrease in the cross sectional area. This is called diffuse necking. In sheet metal, thickness thinning or localized necking in diffuse area may appear if the material continues to be loaded in the tensile direction. The diffuse necking normally appears in stress triaxiality ranges of $0<{\sigma }^{*}\le \frac{2}{3}$ and localized necking in the range of $\frac{1}{3}\le {\sigma }^{*}\le \frac{2}{3}$.

Figure 12. Sketch of Diffuse Necking and Localized

The material will start to weaken due to diffuse necking when the instability strain is reached. The reduced stress in the material is:(12) $${\sigma }_{reduced}=\sigma \cdot \left(1-{\left(\frac{D_{instability}-inst\_start}{1-inst\_start}\right)}^{Fad\_\exp }\right)$$

Where,(13) $D_{instability}={\displaystyle \sum \frac{\text{Δ}{\epsilon }_p}{{\epsilon }_f}}$

In a uniaxial tensile test ${\sigma }^{*}=\frac{1}{3}$.

• If material instability is not included then damage is calculated using the red failure curve in Figure 13
• If material instability is included and modeled using the curve input (table_ID₂) then:
  • Damage due to diffuse necking starts when the plastic strain defined by the blue curve in Figure 13 is reached.
  • Damage due to diffuse necking is linear if Fad_exp=1 is used. Increasing the Fad_exp leads to more energy dissipated during damage. Figure 13 shows the influence of Fad_exp from 1 to 10 in stress-strain curve. It is recommend to use a Fad_exp value of 5 to 10.
  • Once the strain reaches the red curve the element fails.

    
    
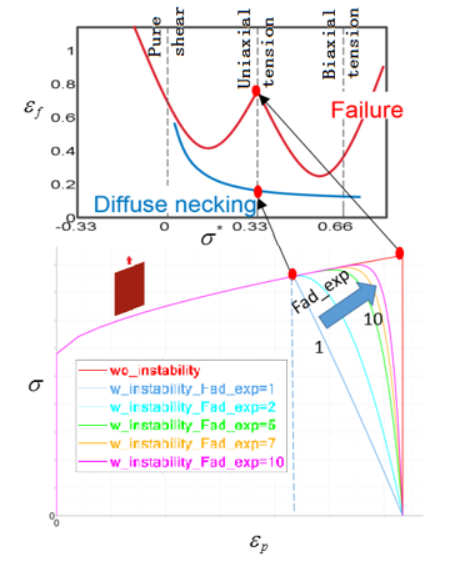
    Figure 13. Influence of Parameter Fad_exp and Material Instability Region

• If only Inst_start is used without curve input in table_ID₂, then the diffuse necking plastic strain is the constant value, Inst_start, for all stress triaxiality.

  
  
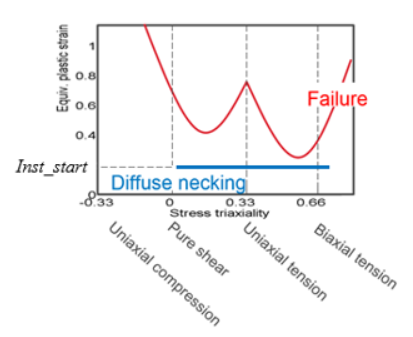
  Figure 14. Constant Inst_start Describing Diffuse Necking