/INTER/LAGDT/TYPE7
Block Format Keyword Describes the interface TYPE7 with constant minimum time step. Which means same behavior as interface TYPE7 with possible switch to Lagrange multiplier formulation, if minimum time step defined with /DT/INTER/CST is reached.
Description
- Same limitation as interface TYPE7 with Lagrange Multiplier formulation.
- Friction is not working after switching into Lagrange Multiplier formulation.
- Not yet compatible with SPMD.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /INTER/LAGDT/TYPE7/inter_ID/unit_ID | |||||||||
| inter_title | |||||||||
| grnd_IDs | surf_IDm | Istf | Igap | Ibag | Idel | ||||
| Fscalegap | Gapmax | ||||||||
| Stmin | Stmax | ||||||||
| Stfac | Fric | Gapmin | Tstart | Tstop | |||||
| IBC | Inacti | VISs | VISF | Bumult | |||||
| Ifric | Ifiltr | Xfreq | Iform | ||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| C6 | |||||||||
Definitions
| Field | Contents | SI Unit Example |
|---|---|---|
| inter_ID | Interface
identifier. (Integer, maximum 10 digits) |
|
| unit_ID | Unit Identifier. (Integer, maximum 10 digits) |
|
| inter_title | Interface
title. (Character, maximum 100 characters) |
|
| grnd_IDs | Secondary nodes group
identifier. (Integer) |
|
| surf_IDm | Main surface
identifier. (Integer) |
|
| Istf | Stiffness definition flag.
4
(Integer) |
|
| Igap | Gap/element option flag.
(Integer) |
|
| Ibag | Airbag vent holes closure
flag in case of contact.
(Integer) |
|
| Idel | Node and segment deletion
flag. 2
(Integer) |
|
| Fscalegap | Gap scale
factor. Default = 1.0 (Real) |
|
| Gapmax | Maximum gap.
(Real) |
|
| Stmin | Minimum
stiffness. (Real) |
|
| Stmax | Maximum
stiffness. Default = 1030 (Real) |
|
| Stfac | Interface stiffness, if
Istf =
1. Default = 0 (Real) |
|
| Stiffness scale factor for
the interface, if Istf =
0. Default = 1.0 (Real) |
||
| Fric | Coulomb
friction. (Real) |
|
| Gapmin | Minimum gap for impact
activation. (Real) |
|
| Tstart | Start
time. (Real) |
|
| Tstop | Time for temporary
deactivation. (Real) |
|
| IBC | Deactivation flag of
boundary conditions at impact. (Boolean) |
|
| Inacti | Deactivation flag of
stiffness in case of initial penetrations. 8
(Integer) |
|
| VISs | Critical damping
coefficient on interface stiffness. Default set to 0.05 (Real) |
|
| VISF | Critical damping
coefficient on interface friction. 16
Default set to 1.0 (Real) |
|
| Bumult | Sorting factor. 11
12
Default set to 0.20 (Real) |
|
| Ifric | Friction formulation flag.
15
(Integer) |
|
| Ifiltr | Friction filtering flag.
16
(Integer) |
|
| Xfreq | Filtering
coefficient. Should have a value between 0 and 1. (Real) |
|
| Iform | Friction penalty
formulation type.
(Integer) |
|
| C1 | Friction law
coefficient. (Real) |
|
| C2 | Friction law
coefficient. (Real) |
|
| C3 | Friction law
coefficient. (Real) |
|
| C4 | Friction law
coefficient. (Real) |
|
| C5 | Friction law
coefficient. (Real) |
|
| C6 | Friction law
coefficient. (Real) |
Flags for Deactivation of Boundary Conditions: IBC
| (1)-1 | (1)-2 | (1)-3 | (1)-4 | (1)-5 | (1)-6 | (1)-7 | (1)-8 |
|---|---|---|---|---|---|---|---|
| IBCX | IBCY | IBCZ |
Definitions
| Field | Contents | SI Unit Example |
|---|---|---|
| IBCX | Deactivation flag of X
boundary condition at impact
(Boolean) |
|
| IBCY | Deactivation flag of Y
boundary condition at impact
(Boolean) |
|
| IBCZ | Deactivation flag of Z
boundary condition at impact
(Boolean) |
Comments
- For the flag Ibag, refer to the monitored volume option (Monitored Volumes (Airbags)).
- Flag Idel = 1 has a CPU cost higher than Idel = 2.
- If Igap = 2, the
variable gap is computed as:
(1) The values given in Line 4 are ignored if Igap ≠ 2.
- Contact stiffness computed
as:
- For Istf = 0,
stiffness
- For Istf > 1,
stiffness
(2) Where,-
is computed from both main
segment stiffness
and secondary node stiffness
Istf = 2,
Istf = 3,
Istf = 4,
Istf = 5,
-
is main segment stiffness and computed as:
When main segment lies on a shell or is shared by shell and solid(3) When main segment lies on a solid:(4) Where,- Segment area
- Volume of the solid
- Bulk modulus
- An equivalent nodal stiffness considered for
interface TYPE7, and computed as:
- When node is connected to a shell
element:
(5) - When node is connected to a solid
element:
(6)
- When node is connected to a shell
element:
-
is computed from both main
segment stiffness
and secondary node stiffness
There is no limitation to the value of stiffness factor (but a value larger than 1.0 can reduce the initial time step).
- For Istf = 0,
stiffness
- The values given in Line 5 are ignored if Istf < 1.
- A default value for Gapmin is computed as the minimum
of:
(7) Where,- Average thickness of the main shell elements
- Average side length of the main brick elements
- The smallest side length of all main segments (shell or brick)
- The gap is computed for each
impact as:
(8) Where,-
: main element gap:
(9) with : thickness of the main element for shell elements
= 0 for brick elements
-
: secondary node gap:= 0 if the secondary node is not connected to any element or is only connected to brick or spring elements.
(10) With being the largest thickness of the shell elements connected to the secondary node.
for truss and beam elements, with being the cross section of the element.
If the secondary node is connected to multiple shells and/or beams or trusses, the largest computed secondary gap is used.
The variable gap is always at least equal to Gapmin.
-
: main element gap:
- Deactivation of the boundary condition is applied to secondary nodes group (grnd_IDs)
- Inacti = 3 may
create initial energy if the node belongs to a spring element.
Inacti = 5 is recommended for airbag simulation deployment
Inacti = 6 is recommended instead of Inacti =5, in order to avoid high frequency effects into the interface.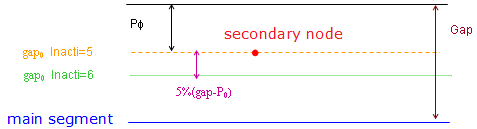
Figure 1. - The sorting factor, Bumult is used to speed up the sorting algorithm.
- The default value for Bumult is automatically increased to 0.30 for models which have more than 1.5 million nodes and to 0.40 for models with more than 2.5 million of nodes.
- One node can belong to the two surfaces at the same time.
- There is no limitation value to the stiffness factor (but a value larger than 1.0 can reduce the initial time step).
- For Friction Formulation
- If the friction flag Ifric =
0 (default), the old static friction formulation is used:
with ( is Coulomb Friction coefficient)
- For flag Ifric >
0, new friction models are introduced. In this
case, the friction coefficient is set by a function
Where,
- Pressure of the normal force on the main segment
- Tangential velocity of the secondary node
- If the friction flag Ifric =
0 (default), the old static friction formulation is used:
- Currently, the coefficients
C1 through C6 are used to define a variable
friction coefficient
for new friction formulations.The following formulations are available:
- Ifric =
1 (Generalized viscous friction
law):
(11) - Ifric =
2 (Modified Darmstad law):
(12) - Ifric =
3 (Renard law):
(13) (14) (15) Where,
- First critical velocity = must be different to 0 (C5 ≠ 0).
- First critical velocity must be lower than the second critical velocity .
- The static friction coefficient C1 and the dynamic friction coefficient C2, must be lower than the maximum friction coefficient C2 (C4 ≤ C1 and C4 ≤ C2).
- Ifric =
1 (Generalized viscous friction
law):
- Friction FilteringIf Ifiltr ≠ 0 , the tangential forces are smoothed using a filter:
(16) Where α coefficient is calculated from:- If Ifiltr = 1 ➤ , simple numerical filter
- If Ifiltr = 2 ➤ standard -3dB filter, with and is filtering period
- If Ifiltr = 3 ➤ standard -3dB filter, with Xfreq is cutting frequency
The filtering coefficient Xfreq should have a value between 0 and 1.
- Friction penalty formulation
Iform
- If Iform =
1, (default) viscous formulation, the friction
forces are:
(17) - While an adhesion force is computed as:
(18) - If Iform =
2, stiffness formulation, the friction forces
are:
(19) - While an adhesion force is computed as:
(20) Where, is contact tangential velocity.
- If Iform =
1, (default) viscous formulation, the friction
forces are: