/MAT/LAW83

Block Format Keyword This law describes the Connection material, which can be used to model spotweld, welding line, glue, or adhesive layers in laminate composite material.

Elastic and elastoplastic behavior can be defined. The plastic behavior of the material can be coupled in normal and shear directions for corresponding displacement-rates. This material is applicable only to solid hexahedron elements (/BRICK) and the element time-step does not depend on element height.

Format

(1)	(2)	(3)	(5)	(6)	(7)	(9)
/MAT/LAW83/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$ $ρ_{i}$
`E`		`G`	`Imass`	`Icomp`	`Ecomp`
`fct_ID`₁		`Y_scale`₁	`X_scale`₁		α	$β$ $β$
`R`_N		`R`_S	`F`_smooth	`F`_cut
`fct_ID`_N	`fct_ID`_S	`XSCALE`

Definitions

Field	Contents	SI Unit Example
`mat_ID`	Material identifier. (Integer, maximum 10 digits)
`unit_ID`	Unit Identifier. (Integer, maximum 10 digits)
`mat_title`	Material title. (Character, maximum 100 characters)
$ρ_{i}$ $ρ_{i}$	Initial density. (Real)	$[\frac{kg}{m^{3}}]$ $[\frac{kg}{m^{3}}]$
`E`	Young's (stiffness) modulus per unit length in tension. (Real)	$[\frac{P a}{m}]$ $[\frac{P a}{m}]$
`G`	Shear (stiffness) modulus per unit length. Default = `E` (Real)	$[\frac{P a}{m}]$ $[\frac{P a}{m}]$
`Imass`	Mass calculation flag. = 0 (Default) Element mass is calculated using density and volume. = 1 Element mass is calculated using density and (means of upper and lower) area. (Integer)
`Icomp`	Compression behavior flag. = 0 Symmetric elasto-plastic behavior in tension and compression. = 1 Linear elastic in compression, elasto-plastic behavior in tension. Default = 0 (Integer)
`Ecomp`	Young’s modulus per unit length in compression. Default = E (Real)	$[\frac{P a}{m}]$ $[\frac{P a}{m}]$
`fct_ID`₁	Normalized yield curve that specifies true stress versus plastic displacement. (Integer)
`Y_scale`₁	Scale factor for ordinate of the normalized function, `fct_ID`₁. 10 Default = 1.0 (Real)
`X_scale`₁	Scale factor for abscissa of the function, `fct_ID`₁. 10 Default = 1.0 (Real)	$[m]$ $[m]$
$α$ $α$	Parameter used in the calculation of the effective true stress. 8 Default = 0.0 (Real)
$β$ $β$	Exponent used in the calculation of the effective true stress. 8 Default = 2.0 (Real)
`R`_N	Maximum true stress in normal direction used in the calculation of effective true stress. Default = 1.0 (Real)	$[Pa]$ $[Pa]$
`R`_S	Maximum true stress in shear direction used in the calculation of effective true stress. Default = 1.0 (Real)	$[Pa]$ $[Pa]$
`F`_smooth	Displacement rate filtering flag. = 0 (Default) No displacement rate filtering. = 1 Displacement rate filtering. (Integer)
`F`_cut	Cutoff frequency for the displacement rate filtering. Default = 10³⁰ (Real)	$[Hz]$ $[Hz]$
`fct_ID`_N	Function identifier defining a scale factor versus the plastic displacement rate in normal direction. 9 Default = 0 (Integer)
`fct_ID`_S	Function identifier defining a scale factor versus the plastic displacement rate in shear direction. 9 Default = 0 (Integer)
`XSCALE`	Scale factor for the abscissa of functions `fct_ID`_N and `fct_ID`_S. 9 Default = 1.0 (Real)	$[\frac{m}{s}]$ $[\frac{m}{s}]$

Example (Connect)

In this example, normal yield curve is fct_ID₁=200. Maximum normal true stress is 0.2 Gpa and maximum shear true stress is 0.4 Gpa.

β = 2

$β = 2$ which is used to fit the mixed-mode load case (30° or 60°) of connection.

α = 0

$α = 0$ , peel effect is not considered.

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1 
unit for mat
                  kg                  mm                  ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW83/1/1
CONNECT MATERIAL
#              RHO_I
              7.8E-6
#                  E                   G     Imass     Icomp               Ecomp 
                  20                             0         0
#  Fct_ID1                      Y_scale1            X_scale1               ALPHA                BETA
       200                             1                   1                   0                   2
#                 RN                  RS   Fsmooth                Fcut
                  .2                  .4         0                   0
#  Fct_IDN   Fct_IDS              XSCALE
         0         0                   0
/FAIL/SNCONNECT/1/1
#            ALPHA_0              BETA_0             ALPHA_F              BETA_F  Ifail_so      ISYM
                   0                   2                   0                   2         1         1
#   Fct_0N    Fct_0S    Fct_FN    Fct_FS            XSCALE_0            XSCALE_F           AREAscale
      2001      2002      2003      2004                   1                   1                   0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  3. FUNCTIONS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/200
MAT83 curve
#                  X                   Y
                   0                   1                                                            
                   1                   1                                                            
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/2001
Fct_0N
#                  X                   Y
                   0                  .5                                                            
                   1                  .5                                                            
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/2002
Fct_0S
#                  X                   Y
                   0                  .5                                                            
                   1                  .5                                                            
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/2003
Fct_fN
#                  X                   Y
                   0                   1                                                            
                   1                   1                                                            
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/2004
Fct_fS
#                  X                   Y
                   0                   1                                                            
                   1                   1                                                            
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

Comments

This law is compatible with 8-noded hexahedron elements (/BRICK) only. It is only compatible with /PROP/TYPE43.
Stiffness modulus and yield curve:
- The stiffness modulus and stresses are defined per displacement in order to be independent from the initial height of the solid element.
  For example, $E$ $E$ =210000 MPa/mm means that the normal stress increases by 210000 MPa for each 1 mm of displacement until the yield stress limit specified by the yield stress curve is reached.
- The stiffness in shear direction is assumed to be equal to the stiffness modulus, $E$ $E$ (Figure 1).
- The Poisson's ratio is equal to zero.
- After reaching the yield stress (defined in fct_ID₁1), the material goes into the plastic phase. After reach the maximum stress R_N (in tension) or R_S (in shear), the stress in material will not increase (Figure 1).
  
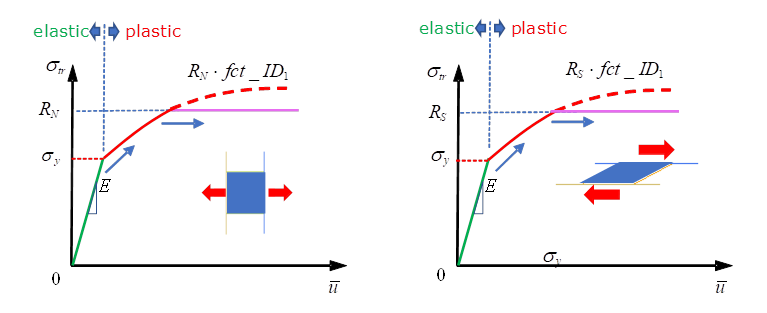
  Figure 1.
- The plastic displacement is accounted for when fct_ID₁ is specified. This is usually a non-decreasing function, which represents true stress as a function of the plastic displacement. The first abscissa value of the function should be “0” and the first ordinate value is the "yield stress". The function may have a stress decrease portion to model material damage.
  
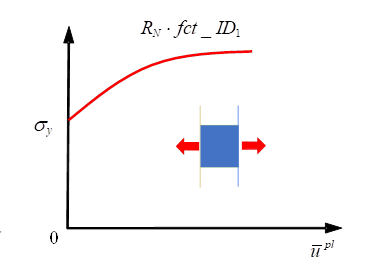
  Figure 2.
Plastic displacement.
The complete element displacement $\bar{u}$ $\bar{u}$ can be subdivided into an elastic portion ${\bar{u}}^{e}$ ${\bar{u}}^{e}$ (before yield stress is reached) and a portion of the plastic displacement ${\bar{u}}^{p l}$ ${\bar{u}}^{p l}$ . In the simplest case of uni-axial tension and compression, plastic displacement is calculated as:(1)
${\bar{u}}^{p l} = \bar{u} - {\bar{u}}^{e} = \bar{u} - \frac{σ_{t r}}{E}$ ${\bar{u}}^{p l} = \bar{u} - {\bar{u}}^{e} = \bar{u} - \frac{σ_{t r}}{E}$

Total normal displacement is the sum of plastic normal displacement and elastic normal displacement.
The material behavior is identical in tension and compression. The normal and shear DOF are not coupled in the elastic region.
The normal and shear DOF are coupled in the plastic region. The normalized effective true stress ( $σ_{y}$ $σ_{y}$ ) is calculated from normal ( $σ_{n}$ $σ_{n}$ ) and shear stress ( $σ_{s}$ $σ_{s}$ ), as:(2)
$σ_{y} = {[{(\frac{σ_{n}}{R_{N} \cdot f_{N} (1 - α \cdot sym)})}^{β} + {(\frac{σ_{s}}{R_{S} \cdot f_{S}})}^{β}]}^{\frac{1}{β}}$ $σ_{y} = {[{(\frac{σ_{n}}{R_{N} \cdot f_{N} (1 - α \cdot sym)})}^{β} + {(\frac{σ_{s}}{R_{S} \cdot f_{S}})}^{β}]}^{\frac{1}{β}}$

Where,

$f_{N}$ $f_{N}$ and $f_{S}$ $f_{S}$

Functions of fct_ID_N and fct_ID_S.

fct_ID_N and fct_ID_S

Specify a scaling coefficient for normal and shear stress as a function of the plastic displacement rate.

$sym$ $sym$

$\sin A$ $\sin A$

$A$ $A$

The angle between the normal of the lower surface and the normal of the upper surface of the solid element.

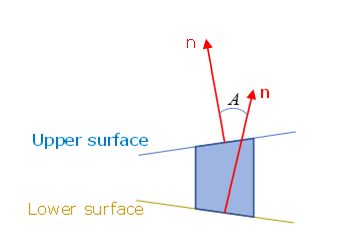
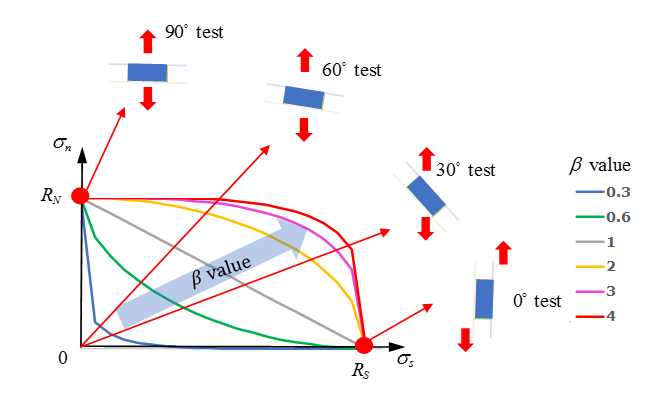
Figure 3.

$α$ $α$

Scale factor used to describe the moment effect (like in the peeling test)

$β$ $β$

Can be fitted with normal and shear combined test. Like the 60° test or the 30° test.

At least one combined test is needed to fit the parameter $β$ $β$ . Figure 4 shows the effect of $β$ $β$ on maximum stress in the combined test.

Figure 4.
The height of the solid element can be equal to zero. The element height does not affect the time step. Only nodal time step is available for this material.
All nodes of the solid elements must be connected to other shells or solid elements, secondary nodes of rigid body (/RBODY) or secondary nodes of tied interface (/INTER/TYPE2).
When all nodes of the solid element become free, the element is deleted.
The rupture criteria for this material is defined by /FAIL/SNCONNECT.
The true stress will be taken from fct_ID₁ as:(3)
$Y = Y_s c a l e_{1} \cdot f_{1} (\frac{X}{X_s c a l e_{1}})$ $Y = Y_s c a l e_{1} \cdot f_{1} (\frac{X}{X_s c a l e_{1}})$

With, $f_{1}$ $f_{1}$ being the function of fct_ID₁