This law models an elasto-plastic material with:
- Isotropic and kinematic hardening
- Tensile rupture criteria
The damage is neglected in the model. The work hardening model is similar to the
Johnson-Cook model (LAW2) without temperature effect where the only difference is in the
strain rate dependent formulation. The equation that describes the stress during plastic
deformation is:
(1)
Where,
-
- Flow stress (Elastic + Plastic Components)
-
- Plastic strain (True strain)
-
- Yield stress
-
- Hardening modulus
-
- Hardening exponent
-
- Strain rate coefficient
-
- Strain rate
-
- Strain rate exponent
The implanted model in Radioss allows the cyclic hardening with
a combined isotropic-kinematic approach.
The coefficient Chard
varying between zero and unity is introduced to regulate the weight between isotropic and
kinematic hardening models.
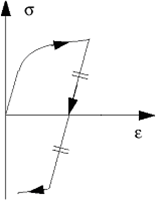
In isotropic hardening model, the yield surface inflates without moving in the space of
principle stresses. The evolution of the equivalent stress defines the size of the yield
surface, as a function of the equivalent plastic strain. The model can be represented in one
dimensional case as shown in
Table 1. When the loading direction is changed, the material is unloaded and the
strain reduces. A new hardening starts when the absolute value of the stress reaches the
last maximum value (
Table 1 (a)).
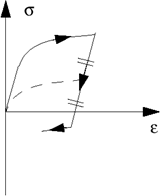
Table 1. Isotropic and Kinematic Hardening Models for Deformation Decrease
| (a) Isotropic
hardening |
(b)
Prager-Ziegler kinematic hardening |
|
|
This law is available for solids and shells. Refer to the Radioss Reference Guide for more information about
element/material compatibilities.

