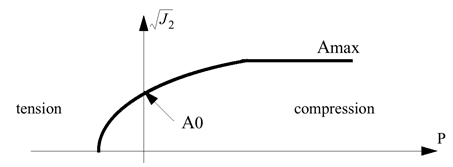
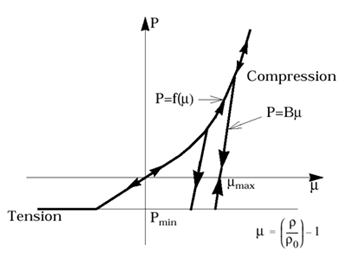
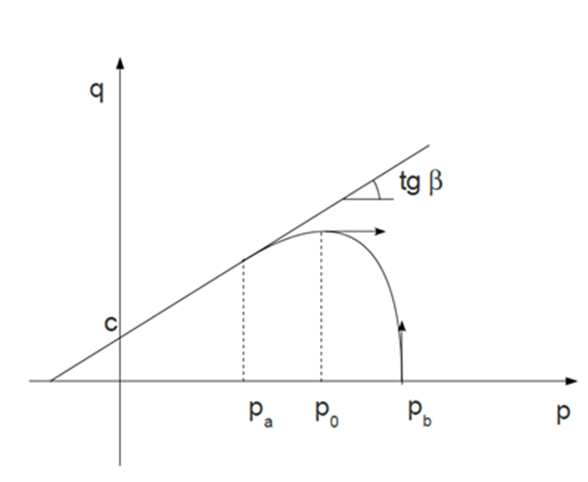
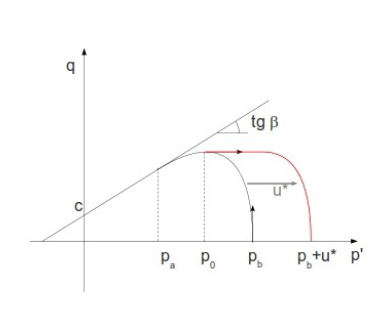
Yield Surface
The Drucker-Prager yield surface is:
(5)
F
=
q
−
r
c
(
p
)
⋅
(
p
tan
β
+
c
)
=
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOraiabg2
da9iaadghacqGHsislciGGYbWaaSbaaSqaaiaacogaaeqaaOWaaeWa
aeaacaWGWbaacaGLOaGaayzkaaGaeyyXIC9aaeWaaeaacaWGWbGaci
iDaiaacggacaGGUbGaeqOSdiMaey4kaSIaam4yaaGaayjkaiaawMca
aiabg2da9iaaicdaaaa@4B01@
Figure 4.
Cap hardening considered in this material law in
p
a
<
p
<
p
b
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGHbaabeaakiabgYda8iaadchacqGH8aapcaWGWbWaaSba
aSqaaiaadkgaaeqaaaaa@3D0C@
is described with:
(6)
r
c
(
p
) =
1 −
(
p −
p
a
p
b
−
p
a
)
2
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciOCamaaBa
aaleaacaGGJbaabeaakmaabmaabaGaamiCaaGaayjkaiaawMcaaiab
g2da9maakaaabaGaaGymaiabgkHiTmaabmaabaWaaSaaaeaacaWGWb
GaeyOeI0IaamiCamaaBaaaleaacaWGHbaabeaaaOqaaiaadchadaWg
aaWcbaGaamOyaaqabaGccqGHsislcaWGWbWaaSbaaSqaaiaadggaae
qaaaaaaOGaayjkaiaawMcaamaaCaaaleqabaGaaGOmaaaaaeqaaaaa
@48CC@
In lower compression or tension
p
≤
p
a
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaiabgs
MiJkaadchadaWgaaWcbaGaamyyaaqabaaaaa@3AA7@
, then linear yield surface will be considered
with:
(7)
r
c
(
p
)
=
1
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciOCamaaBa
aaleaacaGGJbaabeaakmaabmaabaGaamiCaaGaayjkaiaawMcaaiab
g2da9iaaigdaaaa@3C4A@
Where,
q
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyCaaaa@36EC@
von Mises stress
q
2
=
3
J
2
=
3
2
s
i
j
2
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyCamaaCa
aaleqabaGaaGOmaaaakiabg2da9iaaiodacaWGkbWaaSbaaSqaaiaa
ikdaaeqaaOGaeyypa0ZaaSaaaeaacaaIZaaabaGaaGOmaaaacaWGZb
WaaSbaaSqaaiaadMgacaWGQbaabeaakmaaCaaaleqabaGaaGOmaaaa
aaa@41E6@
p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaaaa@36EB@
Pressure
p
=
−
1
3
σ
i
j
=
−
1
3
I
1
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaiabg2
da9iabgkHiTmaalaaabaGaaGymaaqaaiaaiodaaaGaeq4Wdm3aaSba
aSqaaiaadMgacaWGQbaabeaakiabg2da9iabgkHiTmaalaaabaGaaG
ymaaqaaiaaiodaaaGaamysamaaBaaaleaacaaIXaaabeaaaaa@436C@
s
i
j
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4CamaaBa
aaleaacaWGPbGaamOAaaqabaaaaa@38F7@
Deviatoric stress
s
i
j
=
σ
i
j
+
p
δ
i
j
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4CamaaBa
aaleaacaWGPbGaamOAaaqabaGccqGH9aqpcqaHdpWCdaWgaaWcbaGa
amyAaiaadQgaaeqaaOGaey4kaSIaamiCaiabes7aKnaaDaaaleaaca
WGPbaabaGaamOAaaaaaaa@4363@
c
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSbaaSqaai
aacogaaeqaaaaa@3709@
Cohesion
β
Friction angle
p
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaaIWaaabeaaaaa@37D1@
Pressure value
∂ F
∂ p
(
p
0
) = 0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGgbaabaGaeyOaIyRaamiCaaaadaqadaqaaiaadchadaWg
aaWcbaGaaGimaaqabaaakiaawIcacaGLPaaacqGH9aqpcaaIWaaaaa@3FC0@
Plastic Flow
Plastic flow is governed by the non-associated flow potential
G
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4raaaa@36C2@
If
p
≤
p
a
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaiabgs
MiJkaadchadaWgaaWcbaGaamyyaaqabaaaaa@3AA7@
(8)
G
=
q
−
p
⋅
tan
ψ
=
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4raiabg2
da9iaadghacqGHsislcaWGWbGaeyyXICTaciiDaiaacggacaGGUbGa
eqiYdKNaeyypa0JaaGimaaaa@4349@
If
p
a
<
p
≤
p
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGHbaabeaakiabgYda8iaadchacqGHKjYOcaWGWbWaaSba
aSqaaiaaicdaaeqaaaaa@3D90@
(9)
G
=
q
−
tan
ψ
(
p
−
(
p
−
p
a
)
2
2
(
p
0
−
p
a
)
)
=
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4raiabg2
da9iaadghacqGHsislciGG0bGaaiyyaiaac6gacqaHipqEdaqadaqa
aiaadchacqGHsisldaWcaaqaamaabmaabaGaamiCaiabgkHiTiaadc
hadaWgaaWcbaGaamyyaaqabaaakiaawIcacaGLPaaadaahaaWcbeqa
aiaaikdaaaaakeaacaaIYaWaaeWaaeaacaWGWbWaaSbaaSqaaiaaic
daaeqaaOGaeyOeI0IaamiCamaaBaaaleaacaWGHbaabeaaaOGaayjk
aiaawMcaaaaaaiaawIcacaGLPaaacqGH9aqpcaaIWaaaaa@511C@
If
p
>
p
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaiabg6
da+iaadchadaWgaaWcbaGaaGimaaqabaaaaa@39CE@
(example, the flow becomes associated on the
cap)
(10)
G = F
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4raiabg2
da9iaadAeaaaa@3893@
The plastic potential is continuous as you have
∂
G
∂
p
(
p
0
)
=
∂
F
∂
p
(
p
0
)
=
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGhbaabaGaeyOaIyRaamiCaaaadaqadaqaaiaadchadaWg
aaWcbaGaaGimaaqabaaakiaawIcacaGLPaaacqGH9aqpdaWcaaqaai
abgkGi2kaadAeaaeaacqGHciITcaWGWbaaamaabmaabaGaamiCamaa
BaaaleaacaaIWaaabeaaaOGaayjkaiaawMcaaiabg2da9iaaicdaaa a@48D1@
By definition the plastic flow is normal to the flow potential.
(11)
d
ε
i j
p
= d Λ ⋅
∂ G
∂
σ
i j
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabew
7aLnaaDaaaleaacaWGPbGaamOAaaqaaiaadchaaaGccqGH9aqpcaWG
KbGaeu4MdWKaeyyXIC9aaSaaaeaacqGHciITcaWGhbaabaGaeyOaIy
Raeq4Wdm3aaSbaaSqaaiaadMgacaWGQbaabeaaaaaaaa@48B1@
The scalar
d
Λ
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabfU
5ambaa@3854@
Hardening/Softening
The cap is defined by only one parameter
p
b
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGIbaabeaaaaa@37FE@
, assume that
p
a
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGHbaabeaaaaa@37FD@
evolves according to:
(12)
p
a
p
b
=
p
a 0
p
b 0
= α
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca
WGWbWaaSbaaSqaaiaadggaaeqaaaGcbaGaamiCamaaBaaaleaacaWG
IbaabeaaaaGccqGH9aqpdaWcaaqaaiaadchadaWgaaWcbaGaamyyai
aaicdaaeqaaaGcbaGaamiCamaaBaaaleaacaWGIbGaaGimaaqabaaa
aOGaeyypa0JaeqySdegaaa@437B@
Where,
p
a
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGHbGaaGimaaqabaaaaa@38B7@
p
b
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGHbGaaGimaaqabaaaaa@38B7@
Initial value of
p
a
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGHbaabeaaaaa@37FD@
p
b
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGIbaabeaaaaa@37FE@
The evolution of
p
b
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGIbaabeaaaaa@37FE@
depends on
ε
v
p
=
−
ε
i
i
p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyTdu2aa0
baaSqaaiaadAhaaeaacaWGWbaaaOGaeyypa0JaeyOeI0IaeqyTdu2a
a0baaSqaaiaadMgacaWGPbaabaGaamiCaaaaaaa@405C@
via a curve given in input
fct_ID pb .
Note: The same
sign conversion for
ε
v
p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyTdu2aa0
baaSqaaiaadAhaaeaacaWGWbaaaaaa@39BA@
and
p
b
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGIbaabeaaaaa@37FE@
, which is positive in compression is
considered.
Shear yielding has an effect on
p
b
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGIbaabeaaaaa@37FE@
I soft
p
a
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGHbaabeaaaaa@37FD@
p
b
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGIbaabeaaaaa@37FE@
Equation 12 If softening is allowed, the condition
p
a
>
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGHbaabeaakiabg6da+iaaicdaaaa@39C9@
d
ε
v
p
≥ 0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabew
7aLnaaDaaaleaacaWG2baabaGaamiCaaaakiabgwMiZkaaicdaaaa@3D2D@
Derive Stress-Strain Relationships
Considering bulk and shear moduli
K
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4saaaa@36C6@
and
μ
, write the relationship between stress and elastic strain
deviatoric tensors and and between pressure and volumetric strain and its plastic
component.
(13)
d
s
i
j
=
2
μ
(
d
e
i
j
−
d
e
i
j
p
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiaado
hadaWgaaWcbaGaamyAaiaadQgaaeqaaOGaeyypa0JaaGOmaiabeY7a
TnaabmaabaGaamizaiaadwgadaWgaaWcbaGaamyAaiaadQgaaeqaaO
GaeyOeI0IaamizaiaadwgadaqhaaWcbaGaamyAaiaadQgaaeaacaWG
WbaaaaGccaGLOaGaayzkaaaaaa@489A@
(14)
d p = − K (
d
ε
i i
− d
ε
i i
p
) = − K (
d
ε
i i
− d
ε
i i
p
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiaadc
hacqGH9aqpcqGHsislcaWGlbWaaeWaaeaacaWGKbGaeqyTdu2aaSba
aSqaaiaadMgacaWGPbaabeaakiabgkHiTiaadsgacqaH1oqzdaqhaa
WcbaGaamyAaiaadMgaaeaacaWGWbaaaaGccaGLOaGaayzkaaGaeyyp
a0JaeyOeI0Iaam4samaabmaabaGaamizaiabew7aLnaaBaaaleaaca
WGPbGaamyAaaqabaGccqGHsislcaWGKbGaeqyTdu2aa0baaSqaaiaa
dMgacaWGPbaabaGaamiCaaaaaOGaayjkaiaawMcaaaaa@56BA@
Note that,
(15)
∂
G
∂
σ
i
j
=
−
1
3
∂
G
∂
p
δ
i
j
+
3
2
q
s
i
j
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGhbaabaGaeyOaIyRaeq4Wdm3aaSbaaSqaaiaadMgacaWG
QbaabeaaaaGccqGH9aqpcqGHsisldaWcaaqaaiaaigdaaeaacaaIZa
aaamaalaaabaGaeyOaIyRaam4raaqaaiabgkGi2kaadchaaaGaeqiT
dq2aa0baaSqaaiaadMgaaeaacaWGQbaaaOGaey4kaSYaaSaaaeaaca
aIZaaabaGaaGOmaiaadghaaaGaam4CamaaBaaaleaacaWGPbGaamOA
aaqabaaaaa@4FA7@
(16)
∂ F
∂
s
i j
=
∂ G
∂
s
i j
=
3
2 q
s
i j
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGgbaabaGaeyOaIyRaam4CamaaBaaaleaacaWGPbGaamOA
aaqabaaaaOGaeyypa0ZaaSaaaeaacqGHciITcaWGhbaabaGaeyOaIy
Raam4CamaaBaaaleaacaWGPbGaamOAaaqabaaaaOGaeyypa0ZaaSaa
aeaacaaIZaaabaGaaGOmaiaadghaaaGaam4CamaaBaaaleaacaWGPb
GaamOAaaqabaaaaa@4AE7@
You can relate the increment of the plastic volumetric strain
d
ε
v
p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabew
7aLnaaDaaaleaacaWG2baabaGaamiCaaaaaaa@3AA3@
and the equivalent plastic strain
d
ε
d
p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabew
7aLnaaDaaaleaacaWG2baabaGaamiCaaaaaaa@3AA3@
and
d
Λ
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabfU
5ambaa@3854@
.
(17)
d
ε
v
p
= d Λ
∂ G
∂ p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabew
7aLnaaDaaaleaacaWG2baabaGaamiCaaaakiabg2da9iaadsgacqqH
BoatdaWcaaqaaiabgkGi2kaadEeaaeaacqGHciITcaWGWbaaaaaa@42AE@
and
d
ε
d
p
=
d
Λ
∂
G
∂
q
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabew
7aLnaaDaaaleaacaWGKbaabaGaamiCaaaakiabg2da9iaadsgacqqH
BoatdaWcaaqaaiabgkGi2kaadEeaaeaacqGHciITcaWGXbaaaaaa@429D@
∂
G
∂
q
=
1
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGhbaabaGaeyOaIyRaamyCaaaacqGH9aqpcaaIXaaaaa@3C55@
and solving for
d
Λ
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabfU
5ambaa@3854@
from
Equation 11 ,
Equation 14 ,
Equation 16 and
Equation 17 , you
obtain,
(18)
d
Λ
=
1
h
(
∂
F
∂
s
i
j
2
μ
d
e
i
j
−
∂
F
∂
p
K
d
ε
i
i
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabfU
5amjabg2da9maalaaabaGaaGymaaqaaiaadIgaaaWaaeWaaeaadaWc
aaqaaiabgkGi2kaadAeaaeaacqGHciITcaWGZbWaaSbaaSqaaiaadM
gacaWGQbaabeaaaaGccaaIYaGaeqiVd0MaamizaiaadwgadaWgaaWc
baGaamyAaiaadQgaaeqaaOGaeyOeI0YaaSaaaeaacqGHciITcaWGgb
aabaGaeyOaIyRaamiCaaaacaWGlbGaamizaiabew7aLnaaBaaaleaa
caWGPbGaamyAaaqabaaakiaawIcacaGLPaaaaaa@54A0@
With
h = 3 μ + K
∂ F
∂ p
∂ G
∂ p
−
∂ F
∂ c
d c
d
ε
d
p
−
∂ G
∂ p
∂ F
∂
p
b
d
p
b
d
ε
v
p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiAaiabg2
da9iaaiodacqaH8oqBcqGHRaWkcaWGlbWaaSaaaeaacqGHciITcaWG
gbaabaGaeyOaIyRaamiCaaaadaWcaaqaaiabgkGi2kaadEeaaeaacq
GHciITcaWGWbaaaiabgkHiTmaalaaabaGaeyOaIyRaamOraaqaaiab
gkGi2kaadogaaaWaaSaaaeaacaWGKbGaam4yaaqaaiaadsgacqaH1o
qzdaqhaaWcbaGaamizaaqaaiaadchaaaaaaOGaeyOeI0YaaSaaaeaa
cqGHciITcaWGhbaabaGaeyOaIyRaamiCaaaadaWcaaqaaiabgkGi2k
aadAeaaeaacqGHciITcaWGWbWaaSbaaSqaaiaadkgaaeqaaaaakmaa
laaabaGaamizaiaadchadaWgaaWcbaGaamOyaaqabaaakeaacaWGKb
GaeqyTdu2aa0baaSqaaiaadAhaaeaacaWGWbaaaaaaaaa@6444@
You can then compute all terms in Equation 18 .
If
p
≤
p
a
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaiabgs
MiJkaadchadaWgaaWcbaGaamyyaaqabaaaaa@3AA7@
∂
F
∂
p
=
−
tan
β
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGgbaabaGaeyOaIyRaamiCaaaacqGH9aqpcqGHsislciGG
0bGaaiyyaiaac6gacqaHYoGyaaa@40F7@
∂
F
∂
c
=
−
1
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGgbaabaGaeyOaIyRaam4yaaaacqGH9aqpcqGHsislcaaI
Xaaaaa@3D33@
∂
F
∂
p
b
=
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGgbaabaGaeyOaIyRaamiCamaaBaaaleaacaWGIbaabeaa
aaGccqGH9aqpcaaIWaaaaa@3D6F@
If
p
≥
p
a
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaiabgw
MiZkaadchadaWgaaWcbaGaamyyaaqabaaaaa@3AB8@
, then
(19)
∂
F
∂
p
=
−
(
tan
β
r
c
+
d
r
c
d
p
(
p
tan
β
+
c
)
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGgbaabaGaeyOaIyRaamiCaaaacqGH9aqpcqGHsisldaqa
daqaaiGacshacaGGHbGaaiOBaiabek7aIjaadkhadaWgaaWcbaGaam
4yaaqabaGccqGHRaWkdaWcaaqaaiaadsgacaWGYbWaaSbaaSqaaiaa
dogaaeqaaaGcbaGaamizaiaadchaaaWaaeWaaeaacaWGWbGaciiDai
aacggacaGGUbGaeqOSdiMaey4kaSIaam4yaaGaayjkaiaawMcaaaGa
ayjkaiaawMcaaaaa@531D@
∂
F
∂
c
=
−
r
c
(
p
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGgbaabaGaeyOaIyRaam4yaaaacqGH9aqpcqGHsislcaWG
YbWaaSbaaSqaaiaadogaaeqaaOWaaeWaaeaacaWGWbaacaGLOaGaay
zkaaaaaa@410B@
and
∂ F
∂
p
b
=
− p (
p −
p
a
)
r
c
p
b
(
p
b
−
p
a
)
2
(
p tan β + c
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGgbaabaGaeyOaIyRaamiCamaaBaaaleaacaWGIbaabeaa
aaGccqGH9aqpdaWcaaqaaiabgkHiTiaadchadaqadaqaaiaadchacq
GHsislcaWGWbWaaSbaaSqaaiaadggaaeqaaaGccaGLOaGaayzkaaaa
baGaamOCamaaBaaaleaacaWGJbaabeaakiaadchadaWgaaWcbaGaam
OyaaqabaGcdaqadaqaaiaadchadaWgaaWcbaGaamOyaaqabaGccqGH
sislcaWGWbWaaSbaaSqaaiaadggaaeqaaaGccaGLOaGaayzkaaWaaW
baaSqabeaacaaIYaaaaaaakmaabmaabaGaamiCaiGacshacaGGHbGa
aiOBaiabek7aIjabgUcaRiaadogaaiaawIcacaGLPaaaaaa@5890@
If
p
≤
p
a
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaiabgs
MiJkaadchadaWgaaWcbaGaamyyaaqabaaaaa@3AA7@
∂ G
∂ p
= − tan ψ
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGhbaabaGaeyOaIyRaamiCaaaacqGH9aqpcqGHsislciGG
0bGaaiyyaiaac6gacqaHipqEaaa@4125@
If
p
a
≤
p
≤
p
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGHbaabeaakiabgsMiJkaadchacqGHKjYOcaWGWbWaaSba
aSqaaiaaicdaaeqaaaaa@3E41@
, then
(20)
∂ G
∂ p
= − tan ψ
(
p
0
− p
)
(
p
0
−
p
a
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGhbaabaGaeyOaIyRaamiCaaaacqGH9aqpcqGHsislciGG
0bGaaiyyaiaac6gacqaHipqEdaWcaaqaamaabmaabaGaamiCamaaBa
aaleaacaaIWaaabeaakiabgkHiTiaadchaaiaawIcacaGLPaaaaeaa
daqadaqaaiaadchadaWgaaWcbaGaaGimaaqabaGccqGHsislcaWGWb
WaaSbaaSqaaiaadggaaeqaaaGccaGLOaGaayzkaaaaaaaa@4CF1@
If
p
≥
p
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaiabgw
MiZkaadchadaWgaaWcbaGaaGimaaqabaaaaa@3A8C@
∂ F
∂ p
=
∂ G
∂ p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGgbaabaGaeyOaIyRaamiCaaaacqGH9aqpdaWcaaqaaiab
gkGi2kaadEeaaeaacqGHciITcaWGWbaaaaaa@4035@
Finally,
d
q
d
p
=
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca
WGKbGaamyCaaqaaiaadsgacaWGWbaaaiabg2da9iaaicdaaaa@3B83@
gives
(21)
p
0
=
p
a
+
−
(
p
a
tan
β
+
c
)
+
(
p
a
tan
β
+
c
)
2
+
8
[
tan
β
(
p
b
−
p
a
)
]
2
4
tan
β
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaaIWaaabeaakiabg2da9iaadchadaWgaaWcbaGaamyyaaqa
baGccqGHRaWkdaWcaaqaaiabgkHiTmaabmaabaGaamiCamaaBaaale
aacaWGHbaabeaakiGacshacaGGHbGaaiOBaiabek7aIjabgUcaRiaa
dogaaiaawIcacaGLPaaacqGHRaWkdaGcaaqaamaabmaabaGaamiCam
aaBaaaleaacaWGHbaabeaakiGacshacaGGHbGaaiOBaiabek7aIjab
gUcaRiaadogaaiaawIcacaGLPaaadaahaaWcbeqaaiaaikdaaaGccq
GHRaWkcaaI4aWaamWaaeaaciGG0bGaaiyyaiaac6gacqaHYoGydaqa
daqaaiaadchadaWgaaWcbaGaamOyaaqabaGccqGHsislcaWGWbWaaS
baaSqaaiaadggaaeqaaaGccaGLOaGaayzkaaaacaGLBbGaayzxaaWa
aWbaaSqabeaacaaIYaaaaaqabaaakeaacaaI0aGaciiDaiaacggaca
GGUbGaeqOSdigaaaaa@6726@
When
p
<
p
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaiabgY
da8iaadchadaWgaaWcbaGaaGimaaqabaaaaa@39CA@
∂
G
∂
p
<
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGhbaabaGaeyOaIyRaamiCaaaacqGH8aapcaaIWaaaaa@3C51@
Equation 14 is
irrelevant. To achieve this, set
∂
F
∂
p
b
=
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGgbaabaGaeyOaIyRaamiCamaaBaaaleaacaWGIbaabeaa
aaGccqGH9aqpcaaIWaaaaa@3D6F@
d
ε
v
p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabew
7aLnaaDaaaleaacaWG2baabaGaamiCaaaaaaa@3AA3@
d
ε
v
p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabew
7aLnaaDaaaleaacaWG2baabaGaamiCaaaaaaa@3AA3@
For
p
→
p
b
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaiabgk
ziUkaadchadaWgaaWcbaGaamOyaaqabaaaaa@3AE0@
d
r
c
d
p
→
∞
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca
WGKbGaamOCamaaBaaaleaacaWGJbaabeaaaOqaaiaadsgacaWGWbaa
aiabgkziUkabg6HiLcaa@3E40@
d
Λ
→
∞
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabfU
5amjabgkziUkabg6HiLcaa@3BB2@
d
ε
v
p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabew
7aLnaaDaaaleaacaWG2baabaGaamiCaaaaaaa@3AA3@
Equation 17 .
In this case, a special treatment needs to be performed; at first order, the
deviatoric terms are neglected.
(22)
d
ε
v
p
=
−
d
ε
v
(
K
K
+
d
p
b
d
ε
v
p
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabew
7aLnaaDaaaleaacaWG2baabaGaamiCaaaakiabg2da9iabgkHiTiaa
dsgacqaH1oqzdaWgaaWcbaGaamODaaqabaGcdaqadaqaamaalaaaba
Gaam4saaqaaiaadUeacqGHRaWkdaWcaaqaaiaadsgacaWGWbWaaSba
aSqaaiaadkgaaeqaaaGcbaGaamizaiabew7aLnaaDaaaleaacaWG2b
aabaGaamiCaaaaaaaaaaGccaGLOaGaayzkaaaaaa@4C3E@
d
e
i
j
p
=
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiaadw
gadaqhaaWcbaGaamyAaiaadQgaaeaacaWGWbaaaOGaeyypa0JaaGim
aaaa@3C92@
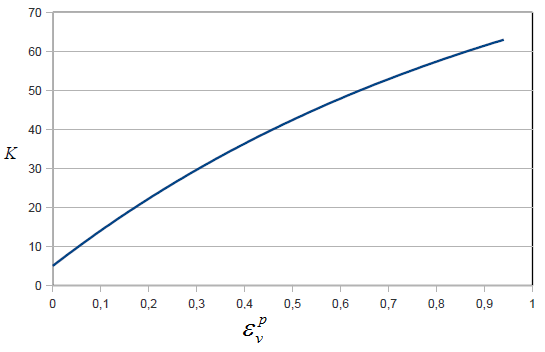
Elastic Properties
Yielding the cap actually models the compaction process. The elastic properties
should thus increase when the porosity decreases, that is,
ε
v
p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyTdu2aa0
baaSqaaiaadAhaaeaacaWGWbaaaaaa@39BA@
The variation of
K
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4saaaa@36C6@
and
μ
with
ε
v
p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyTdu2aa0
baaSqaaiaadAhaaeaacaWGWbaaaaaa@39BA@
are determined by two functions given in input.
Figure 5.
Note: Typically, when variable elastic properties are used, the hardening parameter
ε
v
p
=
∫
d
ε
v
p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyTdu2aa0
baaSqaaiaadAhaaeaacaWGWbaaaOGaeyypa0Zaa8qaaeaacaWGKbGa
eqyTdu2aa0baaSqaaiaadAhaaeaacaWGWbaaaaqabeqaniabgUIiYd
aaaa@4167@
and the volumetric deformation after full
unloading are not consistent.
Porosity Model The porosity model is inspired by
2 and assumes the soils are made of elastic grains
with voids and is for low energies when the soil is not fully compacted. For a fully
compacted soil at high energy, an equation of state should be used. In this material
law, the variation of the volume of voids has an elastic part due to the elastic
deformation of the skeleton and a plastic part which corresponds to the
rearrangement of grains which induces compaction upon pressure loadings and
dilatancy when undergoing shear loadings.
Note: The presence of air is not part of
this model. The porosity is defined so that it represents the volume fraction of
voids, with respect to the total reference volume.
(23)
n
=
V
v
o
i
d
V
t
o
t
a
l
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
GaamOBaiabg2da9iaacckadaWcaaWdaeaapeGaamOva8aadaWgaaWc
baWdbiaadAhacaWGVbGaamyAaiaadsgaa8aabeaaaOqaa8qacaWGwb
WdamaaBaaaleaapeGaamiDaiaad+gacaWG0bGaamyyaiaadYgaa8aa
beaaaaaaaa@445F@
In the elastic case, the void volume does not change.
However, in the plastic case, the porosity change is defined by:
(24)
n
=
1
−
(
1
−
n
0
)
e
ε
v
p
−
ε
v
0
p
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaqaaaaaaaaa
Wdbiaad6gacqGH9aqpcaaIXaGaeyOeI0YaaeWaa8aabaWdbiaaigda
cqGHsislcaWGUbWdamaaBaaaleaapeGaaGimaaWdaeqaaaGcpeGaay
jkaiaawMcaaiaadwgapaWaaWbaaSqabeaapeGaeqyTdu2damaaDaaa
meaapeGaamODaaWdaeaapeGaamiCaaaaliabgkHiTiabew7aL9aada
qhaaadbaWdbiaadAhacaaIWaaapaqaa8qacaWGWbaaaaaaaaa@4A7F@
The initial state of the pores is defined by the initial
porosity, initial saturation, and initial pore pressure. The saturation is defined
as the ratio of the volume of the water to the volume in the void:
(25)
S
=
V
w
a
t
e
r
V
v
o
i
d
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
Gaam4uaiabg2da9iaacckadaWcaaWdaeaapeGaamOva8aadaWgaaWc
baWdbiaadEhacaWGHbGaamiDaiaadwgacaWGYbaapaqabaaakeaape
GaamOva8aadaWgaaWcbaWdbiaadAhacaWGVbGaamyAaiaadsgaa8aa
beaaaaaaaa@4443@
The above voids can be partly or totally filled with water.
In soil mechanics, when the soil is not saturated
S
<
1
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiabgY
da8iaaigdaaaa@388E@
u
=
0
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyDaiabg2
da9iaaicdaaaa@38B1@
S
≥
1
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiabgw
MiZkaaigdaaaa@3950@
u
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyDaaaa@36F1@
3
p
=
p
'
+
u
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaiabg2
da9iaadchadaahaaWcbeqaaiaacEcaaaGccqGHRaWkcaWG1baaaa@3BA5@
p
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaaaa@36EC@
The average density of the void can be calculated
as the mass of the water divided by the volume of the void:
(26)
ρ
v
o
i
d
=
m
w
a
t
e
r
V
v
o
i
d
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyWdi3aaS
baaSqaaiaadAhacaWGVbGaamyAaiaadsgaaeqaaOGaeyypa0ZaaSaa
aeaacaWGTbWaaSbaaSqaaiaadEhacaWGHbGaamiDaiaadwgacaWGYb
aabeaaaOqaaiaadAfadaWgaaWcbaGaamODaiaad+gacaWGPbGaamiz
aaqabaaaaaaa@477A@
Next, define:
(27)
μ
w
=
ρ
v
o
i
d
ρ
w
0
−
1
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
GaeqiVd02damaaBaaaleaapeGaam4DaaWdaeqaaOGaeyypa0ZaaSaa
aeaacqaHbpGCdaWgaaWcbaGaamODaiaad+gacaWGPbGaamizaaqaba
aakeaacqaHbpGCdaWgaaWcbaGaam4DaiaaicdaaeqaaaaakiabgkHi
Tiaaigdaaaa@4548@
Where,
ρ
w
0
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabeg8aYnaaBa
aaleaacaWG3bGaaGimaaqabaaaaa@398E@
For
stability reasons, a viscousity term is added.
If
μ
w
>
−
t
o
l
then
u
v
i
s
=
−
α
v
K
w
ρ
(
V
o
l
)
1
3
ε
v
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8
qacqaH8oqBpaWaaSbaaSqaa8qacaWG3baapaqabaGcpeGaeyOpa4Ja
eyOeI0IaaiiOaiaadshacaWGVbGaamiBaiaabccacaqG0bGaaeiAai
aabwgacaqGUbGaaeiiaiaadwhapaWaaSbaaSqaa8qacaWG2bGaamyA
aiaadohaa8aabeaak8qacqGH9aqpcaGGGcGaeyOeI0IaeqySde2dam
aaBaaaleaapeGaamODaaWdaeqaaOWdbmaakaaapaqaa8qacaWGlbWd
amaaBaaaleaapeGaam4DaaWdaeqaaOWdbiaacckacqaHbpGCaSqaba
GccaGGGcWaaeWaa8aabaWdbiaadAfacaWGVbGaamiBaaGaayjkaiaa
wMcaa8aadaahaaWcbeqaa8qadaWcaaWdaeaapeGaaGymaaWdaeaape
GaaG4maaaaaaGccaGGGcGaeqyTdu2damaaBaaaleaapeGaamODaaWd
aeqaaaaa@5FD8@
u
*
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyDamaaCa
aaleqabaGaaiOkaaaaaaa@37CB@
For a smoother transition,
define:
(28)
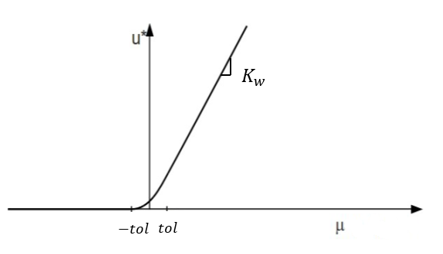
If
μ
w
<
−
t
o
l
:
u
*
=
0
If
|
μ
w
|
<
t
o
l
:
u
*
=
K
w
4
t
o
l
(
μ
w
+
t
o
l
)
2
If
μ
w
>
t
o
l
:
u
*
=
K
w
μ
w
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaaqaaaaa
aaaaWdbiaabMeacaqGMbGaaeiiaiabeY7aT9aadaWgaaWcbaWdbiaa
dEhaa8aabeaak8qacqGH8aapcqGHsislcaWG0bGaam4BaiaadYgaca
GG6aGaamyDa8aadaahaaWcbeqaa8qacaGGQaaaaOGaeyypa0JaaiiO
aiaaicdaaeaacaqGjbGaaeOzaiaabccadaabdaWdaeaapeGaeqiVd0
2damaaBaaaleaapeGaam4DaaWdaeqaaaGcpeGaay5bSlaawIa7aiab
gYda8iaadshacaWGVbGaamiBaiaacQdacaWG1bWdamaaCaaaleqaba
WdbiaacQcaaaGccqGH9aqpcaGGGcWaaSaaa8aabaWdbiaadUeapaWa
aSbaaSqaa8qacaWG3baapaqabaaakeaapeGaaGinaiaadshacaWGVb
GaamiBaaaacaGGGcWaaeWaa8aabaWdbiabeY7aT9aadaWgaaWcbaWd
biaadEhaa8aabeaak8qacqGHRaWkcaWG0bGaam4BaiaadYgaaiaawI
cacaGLPaaapaWaaWbaaSqabeaapeGaaGOmaaaaaOWdaeaapeGaaeys
aiaabAgacaqGGaGaeqiVd02damaaBaaaleaapeGaam4DaaWdaeqaaO
GaeyOpa4ZdbiaadshacaWGVbGaamiBaiaacQdacaWG1bWdamaaCaaa
leqabaWdbiaacQcaaaGcpaGaeyypa0ZdbiaacckacaWGlbWdamaaBa
aaleaapeGaam4DaaWdaeqaaOWdbiaacckacqaH8oqBpaWaaSbaaSqa
a8qacaWG3baapaqabaaaaaa@7D59@
Where,
K
w
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8
qacaWGlbWdamaaBaaaleaapeGaam4DaaWdaeqaaaaa@383C@
is the water bulk modulus.
Figure 6. Pressure, due to Porosity
The cap is then modified by adding a purely von Mises region for
p
0
≤
p
'
≤
p
0
+
u
*
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaaIWaaabeaakiabgsMiJkaadchadaahaaWcbeqaaiaacEca
aaGccqGHKjYOcaWGWbWaaSbaaSqaaiaaicdaaeqaaOGaey4kaSIaam
yDamaaCaaaleqabaGaaiOkaaaaaaa@41B9@
.
Figure 7. Modification to the Cap