grsm

Syntax

x = grsm(@func,x0)

x = grsm(@func,x0,A,b)

x = grsm(@func,x0,A,b,Aeq,beq)

x = grsm(@func,x0,A,b,Aeq,beq,lb,ub)

x = grsm(@func,x0,A,b,Aeq,beq,lb,ub,nonlcon)

x = grsm(@func,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

[x,fval,info,output] = grsm(...)

Inputs

func

The function to minimize.

x0

An estimate of the location of a minimum.

A

A matrix used to compute A*x for inequality contraints.

Use [ ] if unneeded.

b

The upper bound of the inequality constraints A*x<=b.

Use [ ] if unneeded.

Aeq

A matrix used to compute Aeq*x for equality contraints.

Use [ ] if unneeded.

beq

The upper bound of the equality constraints Aeq*x=beq.

Use [ ] if unneeded.

lb

The design variable lower bounds.

Use [ ] if unbounded. Support for this option is limited. See Comments.

ub

The design variable upper bounds.

Use [ ] if unbounded. Support for this option is limited. See Comments.

nonlcon

The non-linear constraints function.

The function signature is as follows:

function [c, ceq] = ConFunc(x)

where c and ceq contain inequality and equality contraints, respectively. The inequality constraints are assumed to have upper bounds of 0.

The function can return 1 or 2 outputs.

options

A struct containing options settings.

See grsmoptimset for details.

Outputs

x

The locations of the multi-objective minima.

fval

The multi-objective function minima.

info

The convergence status flag.

• info = 3: A constraint violation within TolCon occurred.
• info = 0: Reached maximum number of iterations.

output

A struct containing iteration details. The members are as follows.

Pareto

A logical matrix indicating which samples belong to the Pareto Front. Each column contains the front information for an iteration.

nfev

The number of function evaluations.

xiter

The candidate solution at each iteration.

fvaliter

The objective function values at each iteration.

coniter

The constraint values at each iteration. The columns will contain the constraint function values in the following order:

1. linear inequality contraints
2. linear equality constraints
3. nonlinear inequality contraints
4. nonlinear equality constraints

Examples

Plot the iterations and Pareto Front for the function ObjFunc.

function obj = ObjFunc(x)
    obj = zeros(2,1);
    obj(1) = 2*(x(1)-3)^2 + 4*(x(2)-2)^2 + 6;
    obj(2) = 2*(x(1)-3)^2 + 4*(x(2)+2)^2 + 6;
end

init = [2; 0];
lowerBound = [1, -5];
upperBound = [5, 5];

options = grsmoptimset('MaxIter', 50);
[x,fval,info,output] = grsm(@ObjFunc,init,[],[],[],[],lowerBound,upperBound,[],options);

obj1 = output.fvaliter(:,1);
obj2 = output.fvaliter(:,2);
scatter(obj1, obj2);
hold on;

obj1P = fval(:,1);
obj2P = fval(:,2);
scatter(obj1P, obj2P);
legend('Iteration History','Pareto Front');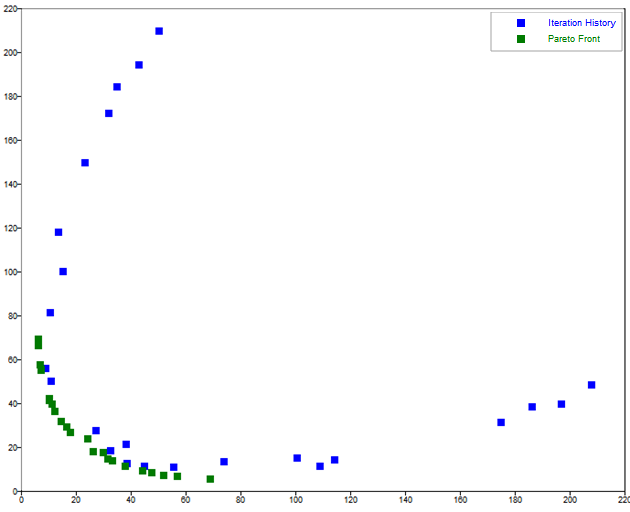

Figure 1. grsm figure 1

function obj = ObjFunc(x,p1,p2)
    obj = zeros(2,1);
    obj(1) = 2*(x(1)-3)^2 + 4*(x(2)-2)^2 + p1;
    obj(2) = 2*(x(1)-3)^2 + 4*(x(2)+2)^2 + p2;
end

handle = @(x) ObjFunc(x,7,8);
[x,fval] = grsm(handle,init,[],[],[],[],lowerBound,upperBound,[],options);

Comments

grsm uses a Global Response Surface Method.

See the fmincon optimization tutorial, Activate-4030: Optimization Algorithms in OML, for an example with nonlinear constraints.

Unbounded limits design variable limits are not fully supported and are set to -1000 and 1000. Use of large limits is discouraged due to the size of the search area.

To pass additional parameters to a function argument, use an anonymous function.