Transient Magnetic: solved equations (introduction)
Introduction
The equations used for the solving are:
- Maxwell's equations (for a magnetic system)
- the constitutive equations of the matter
The computation conditions for a Transient Magnetic application are the following:
- the state variables are time dependent: d/dt ≠ 0 (transient or variable state: current sources vary with time)
- the computation concerns only the B, H and E fields (the D field is not computed). The equations of the electric fields E and D and of the magnetic fields B, H can't be decoupled.
Equations and conditions
In the previously defined conditions of computation, the equations are summarized as follows:
|
|
E : electric field strength (in V/m) B: magnetic flux density (in T) H: magnetic field strength (in A/m) J: current density (in A/m2) |
|||
|
|
σ : conductivity (in S) μ : permeability (in H/m) |
|||
The principal equation for magnetic materials, can be put in form B(H) or H(B) as presented below.
|
|
⇒ |
|
μr : perméabilité relative μ0 : perméabilité du vide Br : induction rémanente (aimants) |
|
|
⇒ |
|
νr : reluctivity νr =1/μr ν0 : vacuum reluctivity ν0 =1/μ0 Hc : coercive magnetic field (permanent magnets) |
Models
To solve these equations, two models are used:
-
the vector model, which uses:
the magnetic vector potential (written
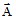 )
) -
the scalar model, which uses:
magnetic scalar potentials (written ϕtot or ϕred)
Model and 2D or 3D application
For 2D applications, the vector model is available by default.
For 3D applications, the scalar model is available by default.