Aerodynamics for Cars and Trucks
Basic Approach
The following is an aerodynamics concept as proposed by Manfred Mitschke and Henning Wallentowitz 1.
The resultant aerodynamic force and torque is considered to act on a reference point Oc placed on the road surface at the center of the four wheels.
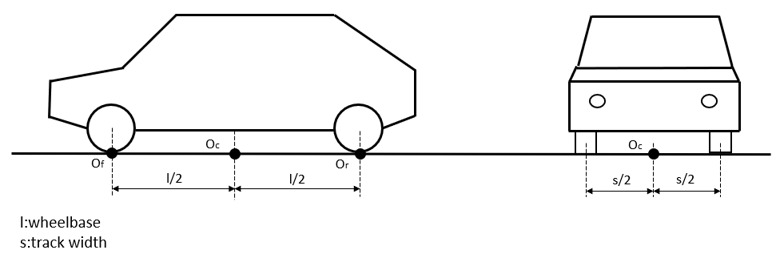
Figure 1.
Fa,x = cx(τL)*P(vr)
Fa,y = cy(τL)*P(vr)
Fa,z = cz(τL)*P(vr)
Ma,x = cmx(τL)*l*P(vr)
Ma,y = cmy(τL)* l*P(vr)
Ma,z = cmz(τL)* l*P(vr)
Where ci express the aerodynamic coefficients, τL the relative airflow incidence angle, vr the resulting velocity, P the dynamic pressure and l the wheelbase.
The coordinate system in which the above defined force and torque components are to be applied is located in Oc and fixed to the car body.
On Velocities
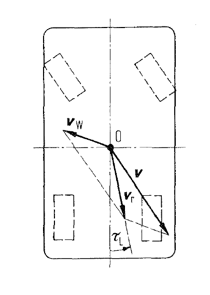
Figure 2.
On P(vr)
The dynamic pressure can be calculated using the air density ρ, the resulting velocity vr, and the following formula.
P(vr) = 0.5 * ρ * vr2
The air density is dependent on the ambient temperature and pressure of the environment, and the ideal gas constant for air and it is often regarded as constant.
Vertical Force and Pitch Torque
The vertical force Fa,z and the pitch torque Ma,y are replaced by two vertical forces acting at the center points of the suspensions Of and Or at ground level introducing cz,f and cz,r.
Fa,zf = cz,f(τL)*P(vr)
Fa,zr = cz,r(τL)*P(vr)The action forces are applied at reference point Oc placed on the road surface at the center of the four wheels and the center points of the suspensions Of and Or at ground level.
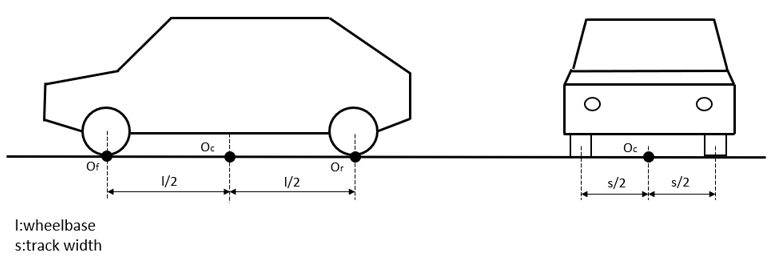 Figure 3.
Figure 3. This aerodynamic system is the default setting in the Assembly Wizard for the Car and Truck Library.
The complete set of aerodynamic forces and torques can be applied to the rigid car body as follows:
Fa,x = 0.5*cx(τL)* ρ * A* vr2
Fa,y = 0.5*cy(τL)* ρ * A* vr2
Fa,zf = 0.5*cz,f(τL)* ρ * A* vr2
Fa,zr = 0.5*cz,r(τL)* ρ * A* vr2
Ma,x = cmx(τL)* l* ρ * A* vr2
Ma,z = cmz(τL)* l* ρ * A* vr2
Where A is the frontal area of the car. Vehicle frontal areas are typically in the range of 1.5 m2 < A < 2.5 m2 for passenger cars and 4 m2 < A < 9 m2 for trucks and buses.
How to Determine ci
As a very rough approximation the ci can be regarded as constants, and to disable aerodynamic totally, all ci can be set to zero.
| τL =0deg | τL =10deg | τL =20deg | τL =30deg | |
|---|---|---|---|---|
| cx | 0.3 | 0.31 | 0.32 | 0.33 |
| cy | 0 | 0.4 | 0.8 | 1.2 |
| cz,f | 0.1 | 0.2 | 0.3 | 0.4 |
| cz,r | 0 | 0.1 | 0.2 | 0.3 |
| cmx | 0 | 0.03 | 0.06 | 0.09 |
| cmz | 0 | 0.04 | 0.08 | 0.12 |
One limitation of using this table is that is does not allow situations where the car is subjected to diagonal airflow of over 30 degrees (some of the curves go up to 40 degrees). Such conditions, especially pure sidewind conditions, will be considered for implementation in future releases.
ci coefficients could be derived by a virtual wind tunnel experiment. The values measured in such an experiment would be the constrained forces at Oc, Or and Of as functions or vr and τ.