Simplified case: filiform conductors
Introduction
This paragraph gives the analytical expression of partial inductance in the simplified case of two filiform parallel conductors (negligible cross-section area).
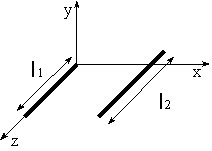
Reminder: The partial inductance between segments S1 and S2 is expressed by the formula:
![]()
Magnetic vector potential
The expression of the magnitude of the vector potential created by a current I1 in a point M of coordinates (x0, y0, z0) is given by the following formula:
![]()
Partial inductance between two conductors
In order to obtain partial inductance between two parallel filiform conductors, we integrate the vector potential created by the current I1 on the conductor and provided with a current I2.
The following analytical expression is obtained:
![]()
where:
![]()
![]()
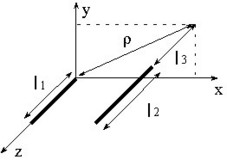
Partial inductance of a conductor
The partial inductance of a filiform conductor can be more difficult to obtain because the previous formula diverges when ρ = 0 and l3 = 0.
It is then necessary to apply the volume formula given in § Real case: volume conductors.