Apply Moments
Create concentrated moments by applying a load, representing moments, to a node or set.
Moments are load config 2 and are displayed with a double-headed vector with the letter M at the tail end.
Equations allow you to create force, moment, pressure, temperature or flux loads on your model where the magnitude of the load is a function of the coordinates of the entity to which it is applied. An example of such a load might be an applied temperature whose intensity dissipates as a function of distance from the application point, or a pressure on a container walls due to the level of a fluid inside.
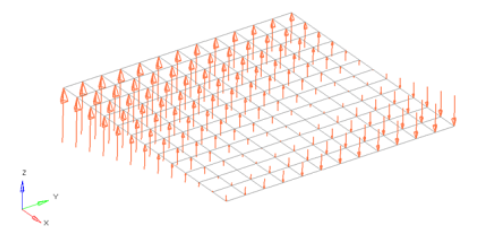
Figure 3. Flat Plate with a Linear Function for an Applied Force Magnitude = 20 – (5*x+2*y). The flat plate is 20 x 20 units, lying in the X-Y plane with the origin at the center.
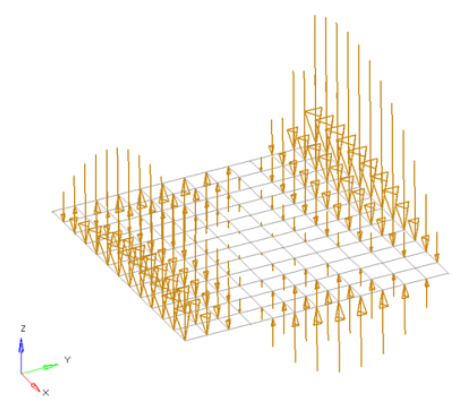
Figure 4. Flat Plate with a Polynomial Function with Magnitude = x^2-2y^2+x*y+x+y. The flat plate is 20 x 20 units, lying in the X-Y plane with the origin at the center.
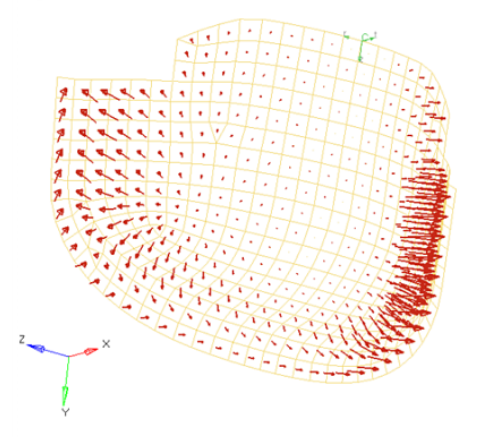
Figure 5. Curved Surface with a Polynomial Function for an Applied Pressure Magnitude = -((x^2+2*y^2+z)/1000). The pressure function is defined in terms of the cylindrical coordinate system displayed at the top edge of the elements.

