Solid Elements (/PROP/SOLID)
Solids hexahedron and tetrahedron with linear and quadratic interpolation functions are available in Radioss.
- TETRA4:
- TETRA10:
- BRICK8:
- BRICK20:
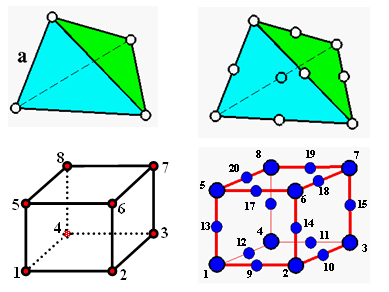
Figure 1. Solid Finite Element Meshes in Radioss
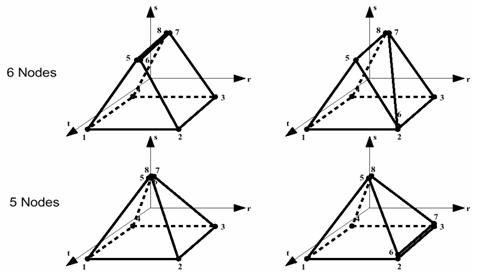
Figure 2. Solid Elements Degeneration Examples
| Mesh | Element Name | Number of Integration Points | Hourglass Formulation | Comments |
|---|---|---|---|---|
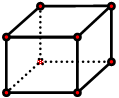 |
BRICK8 | 1x1x1 2x2x2 |
Penalty for the case of 1 IP | Use co-rotational
formulation. Avoid hourglass TYPE 2 |
| HA8 | from 2x2x2 to 9x9x9 | --- | Note the value used for the flag, Icpre | |
| HEPH | 1x1x1 | Physical stabilization | ||
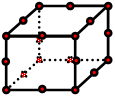 |
BRICK20 | 2x2x2 or 3x3x3 | --- | Too high cost element |
 |
TETRA4 | 1 | --- | Shear locking in large
deformation Low precision element |
 |
TETRA10 | 4 | --- | High cost Good precision without shear locking |