Free-shape optimization

Overview

The first version of free-shape optimization has been implemented in Flux 2021.2. Currently, three types of responses to optimize can be chosen in Flux: flux, torque or force. During the optimization, Flux computes the sensitivities of each responses from the adjoint method on the lines to optimize and then launches OptiStruct to run the free-shape optimization process. To run the free-shape optimization, OptiStruct must be installed and the OptiStruct installation path must be set in the FluxSupervisor Options in the Coupled software section. The free-shape optimization moves the mesh nodes of the line you want to optimize to maximize or minimize your responses. This feature will allow the design of new shapes for your devices and will bring better performances.

Example of application

This example may be seen as an extension of the example available in the supervisor in the 2D Application Note section named: Shape Optimization of a synchronous reluctance machine

Let's consider the modeling of the following electrical machine represented by only one quarter of the full device.

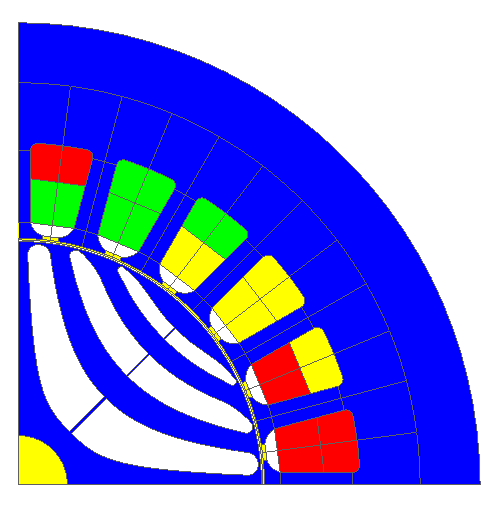
Figure 1. Four poles electrical machine with three current phasis

To run the shape optimization, the selected response is the Torque, a path to compute the torque is depicted in the following figure:

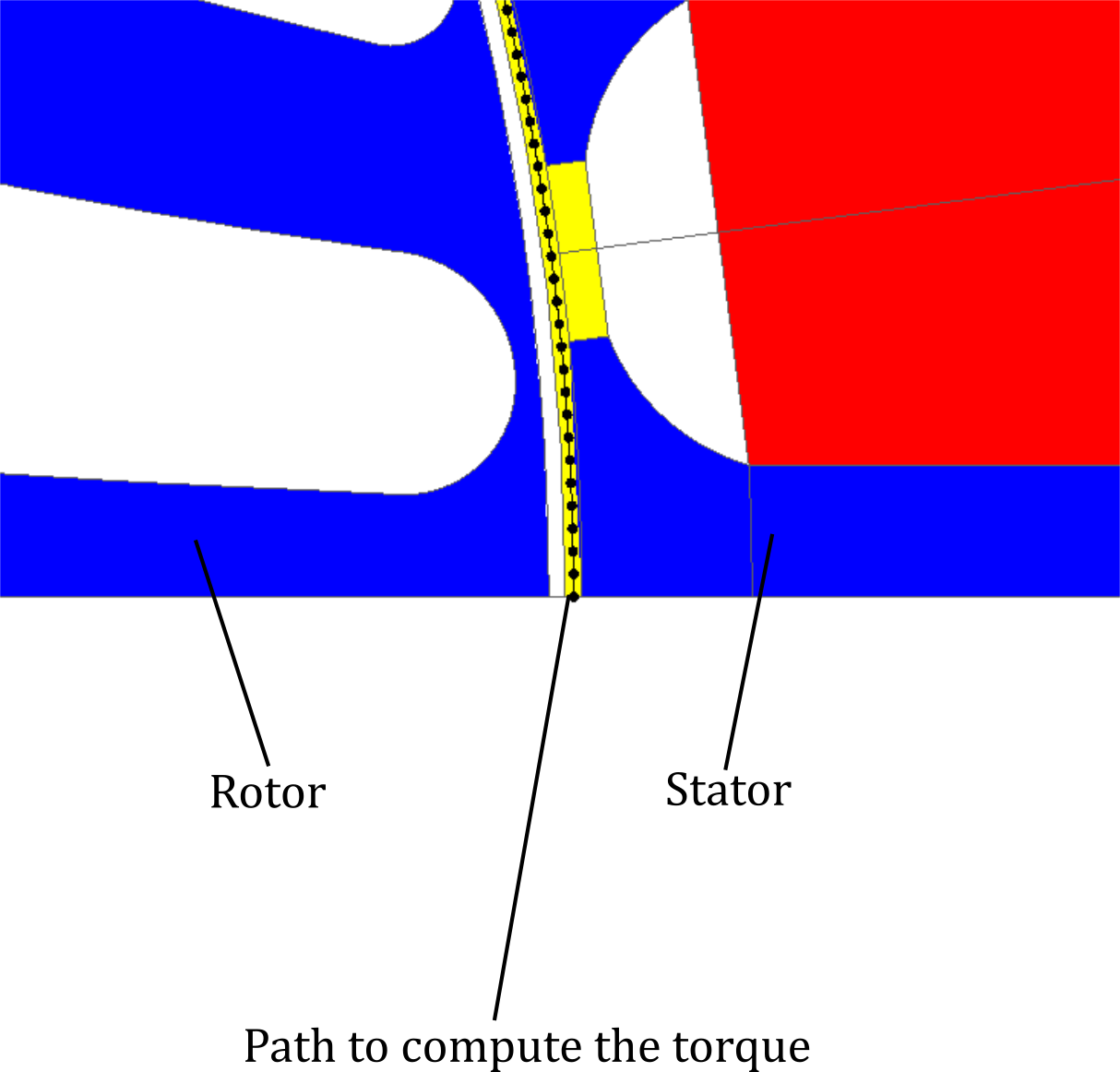
Figure 2. Description of the path to compute the torque with Maxwell's tensor approach

Defined with one point per degree and a radius in the airgap on the stator side, this path ensure to have a good computation of the torque. This motor has four poles.

The symmetry constraint may be setted as follow:

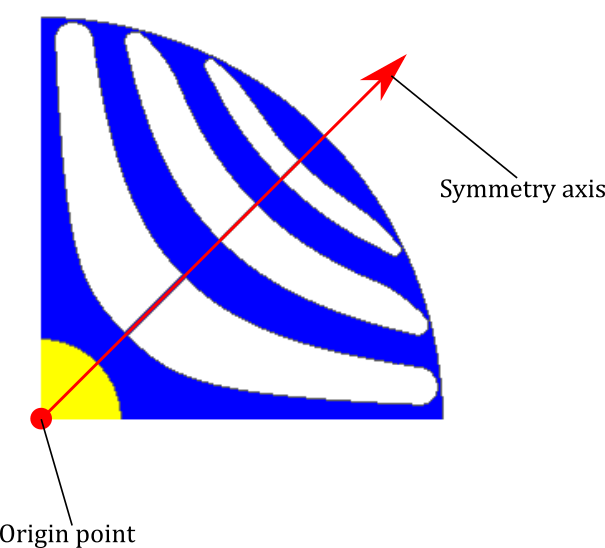
Figure 3. Origin point and symmetry axis for the one axis symmetry constraint

The origin axis is setted to (0,0) and the symmetry axis is setted to (0.5,0.5).

For the constraint on the volume, we want to reduce the volume of iron in the rotor about 20%, in the upper bound the value corresponding to 80% of the total volume is filled, in the lower bound 60% of the volume is filled.

Even if at the starting point the initial design is not between the bounds, the optimization algorithm will deteriorate the objective function in order to find a design that fit the bounds, then the algorithm will start to optimize the design in order to increase or decrease the objective function.

In the objective function, we choose to Maximize the Average of the Torque response previously defined

In the end, the lines where the nodes can move are selected as depicted in the figure bellow (the lines are surrounded in yellow):

Figure 4. Lines to be considered during the optimization process

The scenario is piloted by the mechanical set angle and is covering an electrical period with two degrees per computation step.

Using the Shape Optimization, we obtain several files in the temporary folder (.wmv for HyperView) to see the results, check the mesh of the Project_OptimizationResults.FLU:

Figure 5. Initial design of the reluctance synchronous machine (a) and final design of the reluctance synchronous machine (b)

Even though the initial motor already has good performances, the use of the Shape Optimization brings remarkable improvements. As shown in Table 1, a 4.8% increase of the mean torque is achieved, with a rotor mass reduction of 20%. Figure 5 shows initial and optimized rotor configuration.

Table 1. Comparison between the initial design and the final design of the synchronous reluctance machine

	Initial design	Final design	Difference
Mean torque (N.m)	11.9	12.5	+ 4.8%
Rotor weight (kg)	0.5	0.4	- 20%