Calcul par éléments finis, les fonctions d’approximation
Introduction
Ce paragraphe traite des fonctions d’approximation dans le cadre des applications magnétiques pour les formulations choisies automatiquement (Potentiel scalaire magnétique et potentiel vecteur électrique):
- de l’ordre des fonctions d’approximation : 1er ordre / 2nd ordre
- du type des fonctions d’approximation : arête / nodale
Ordre des éléments et fonctions d’approximation
-
différents types d’ordre pour le maillage : maillage du 1er ordre ou maillage du 2nd ordre
- différents types de fonctions d’approximation : des fonctions linéaires (1er ordre) ou des fonctions quadratiques (2nd ordre)
| Maillage | Position des nœuds | Fonction d’approximation |
|---|---|---|
| 1er ordre | Sommets | Linéaire (polynôme d’ordre1) |
| 2nd ordre | Sommets + milieu des arêtes | Quadratique (polynôme d’ordre2) |
Il est possible de dissocier l’ordre des fonctions d’approximation et l’ordre du maillage. L’utilisateur peut ainsi combiner un maillage au 1er ordre avec des fonctions d’approximation du 2nd ordre et réciproquement*.
Fonction d’approximation nodale ou d’arête
Flux propose à l’utilisateur des fonctions d’approximation :
- d’arêtes (calcul sur les arêtes des éléments et stockage de l’information sur le nœud milieu)
- nodales (calcul aux nœuds des éléments)
Les fonctions d’arêtes sont proposées uniquement pour le potentiel vecteur électrique T. Pour le potentiel scalaire magnétique ϕ, les fonctions d’approximation sont nodales.
L’utilisation des fonctions d’arête s’applique donc aux régions de type conducteur massif (applications Magnétique Transitoire et Magnéto Harmonique).
Attention
- conducteur massif
- présence de courants (induits) tangent à des arêtes du dispositif ces arêtes sont des arêtes de coins rentrants
Exemple : calcul de courants de Foucault dans un conducteur massif passif de type plaque mince en présence de fissures.
Modifier les choix par défaut
L’utilisateur n’a pas besoin de modifier l’ordre ou le type des fonctions d’approximation. Les choix par défaut sont les choix adaptés à la majorité des situations. Cependant, il peut être amené dans certaines conditions particulières à modifier ces choix.
- mode automatique : choix par défaut
- mode manuel : choix de l’utilisateur
En mode automatique
- si le maillage est au 1er ordre, les fonctions d’approximation nodales sont au 1er ordre
- si le maillage est au 2nd ordre, les fonctions d’approximation nodales sont au 2nd ordre
S’il existe des régions de type conducteur massif (formulation en potentiel vecteur électrique), les fonctions d’approximation sont des fonctions d’arêtes qui nécessitent un maillage du second ordre. La génération des éléments du second ordre est alors automatiquement réalisée.
- Potentiel scalaire magnétique : fonction d’approximation nodale (2nd ordre)
- Potentiel vecteur électrique : fonction d’approximation d’arête
En mode manuel
En mode manuel, l’utilisateur peut modifier l’ordre (1er ordre /
2nd ordre) et le type des fonctions d’approximation (nodale / arête pour
le potentiel vecteur électrique). Ces modifications sont réalisées dans la boîte
associée à la définition de l’application comme cela est présentée dans la figure
ci-dessous. 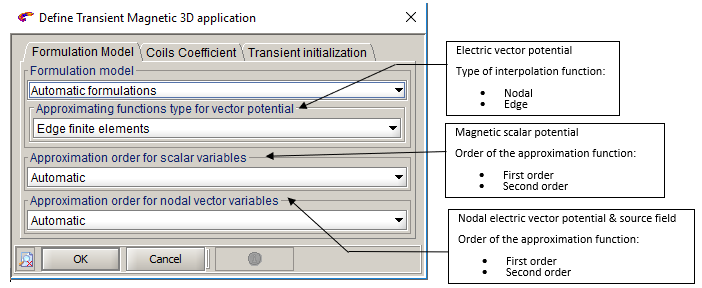
Conseils
Pour un projet de taille conséquente, lorsque la mémoire est insuffisante lors de la résolution, il est possible de diminuer cette mémoire en choisissant l’ordre d’approximation des variables vectorielles au premier ordre. Cela permet de gagner du temps et de la mémoire, en dépit d’une légère dégradation de la précision des résultats.