Magnéto Statique : équations résolues (introduction)
Introduction
Les équations utilisées pour la résolution sont :
- les équations de Maxwell (pour un système magnétique)
- les équations constitutives de la matière
Les conditions de calcul pour une application Magnéto Statique sont les suivantes :
- l'étude est une étude statique : d/dt = 0
- on s'intéresse aux champs B et H (les champs D et E ne sont pas calculés). Les équations en champs magnétiques B, H et en champs électriques E, D sont découplées.
Equations et conditions
Dans les conditions de calcul énoncées précédemment, les équations se résument de la façon suivante :
|
|
|
B : induction magnétique (en T) H : champ magnétique (en A/m) J : densité de courant (en A/m2) |
||
|
μ : perméabilité magnétique (en H/m) | |||
L'équation constitutive de la matière pour les matériaux magnétiques, peut se mettre sous la forme B(H) ou H(B) comme présenté ci-dessous.
|
|
|
μr : perméabilité relative μ0 : perméabilité du vide Br : induction rémanente (aimants) |
ou
|
|
|
νr : réluctivité νr =1/μr ν0 : réluctivité du vide ν0 =1/μ0 Hc : champ coercitif (aimants) |
Les modèles
Pour résoudre ces équations, deux modèles sont utilisables :
-
le modèle vecteur qui utilise :
le potentiel vecteur magnétique (noté
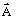 )
) -
le modèle scalaire qui utilise :
des potentiels scalaires magnétiques (notés ϕtot ou ϕred)
Modèle et application 2D ou 3D
Pour les applications 2D (résolues avec le solveur 2D), le seul modèle disponible est le modèle vecteur.
Pour les applications 2D et 3D (résolues avec le solveur 3D), les deux modèles (vecteur et scalaire) sont proposés :
- le modèle vecteur pour les applications 2D
- le modèle scalaire pour les applications 3D