Approximation des modèles en magnéto harmonique
Rappel sur l'application Magnéto Harmonique
Dans Flux, dans une application Magnéto Harmonique , les variables inconnues (potentiels) et les grandeurs physiques qui en dérivent (champ magnétique et induction magnétique) sont supposées varier de façon sinusoïdale en fonction du temps.
La représentation complexe est donc utilisée, et la solution peut être obtenue en une seule résolution .
Problématique
En Magnéto Harmonique la variable d'état varie sinusoïdalement dans le temps, de même que ces grandeurs dérivées : champ magnétique H et induction magnétique B.
Or, dans la réalité, en présence d'un matériau non linéaire, le champ magnétique H et l'induction magnétique B ne varient pas sinusoïdalement simultanément (cf. figure ci-dessous).
| Si B sinusoïdal … | Si H sinusoïdal … |
|---|---|
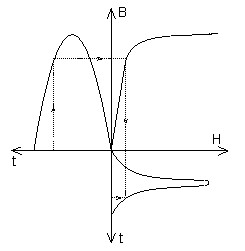
|
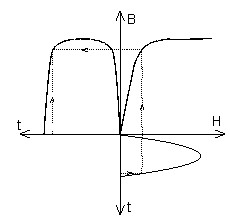
|
| … ⇒ H non sinusoïdal | … ⇒ B non sinusoïdal |
Solution proposée
Afin de prendre en compte les contradictions énoncées précédemment, des approximations sont réalisées au niveau des modèles proposés pour la loi de comportement magnétique.
La caractéristique B(H) est modifiée afin de fonctionner à un niveau d'énergie équivalent. On parle alors de caractéristique B(H) équivalente , ou de méthode basée sur une équivalence énergétique.
Principe de la méthode
L'énergie est représentée par la surface grisée sur la figure ci-dessous.
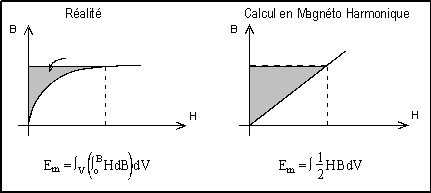
La courbe B(H) équivalente est calculée de telle façon que, en tout point de
l'espace, la densité d'énergie magnétique moyenne par période obtenue à partir de la courbe B(H) réelle, soit égale à la densité d'énergie magnétique donnée par la courbe B(H) équivalente.
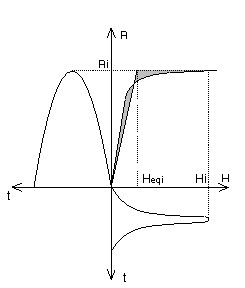
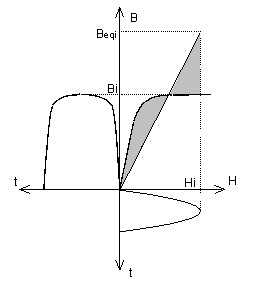
Pour le calcul de la courbe B(H) équivalente, il existe deux cas extrêmes présentés sur la figure ci-dessous.
| B sinusoïdal | H sinusoïdal |
|
|
|
Point de fonctionnement réel : pour B = Bi on a H = Hi La caractéristique équivalente est obtenue en déplaçant le point de fonctionnement pour travailler à énergie équivalente : pour B = Bi on a alors H = Heqi Heqi est calculé de telle sorte qu'il y ait égalité des surfaces grisées. |
Point de fonctionnement réel : pour H = Hi on a B = Bi La caractéristique équivalente est obtenue en déplaçant le point de fonctionnement pour travailler à énergie équivalente : pour H = Hi on a alors B = Beqi Beqi est calculé de telle sorte qu'il y ait égalité des surfaces grisées. |
Principe de la méthode (suite)
Dans la réalité, ni B ni H ne sont sinusoïdaux. Les résultats obtenus avec les courbes équivalentes calculées dans les deux cas extrêmes encadrent le plus souvent le résultat exact. C'est pourquoi, la courbe équivalente peut également être calculée à l'aide d'une combinaison linéaire entre ces deux cas extrêmes (cf. modèles équivalents proposés dans Flux).
Courbes équivalentes
Les courbes équivalentes sont présentées sur la figure ci-dessous.
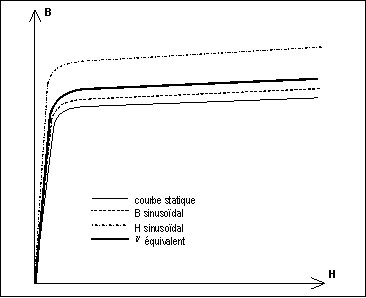
Limites de la méthode
Dans tous les cas, seules les valeurs dépendant de l'énergie sont correctes (force, puissance, inductance, ...).
Les grandeurs instantanées, quant à elles, sont des approximations puisque exprimées sous forme sinusoïdale. Elles peuvent donner tout de même une idée, plus ou moins précise, des résultats.
Bibliographie
Des informations complémentaires sur la modélisation des matériaux magnétiques non linéaires en Magnéto Harmonique sont disponibles dans les documents suivants :
- « Contribution à la modélisation des moteurs asynchrones par la méthode des éléments finis »thèse d'Eric VASSENT – 1990INPG
- « Détermination des pertes par courant de Foucault dans les cuves de transformateursModélisation de régions minces et prise en compte de la saturation des matériaux magnétiques en régime harmonique » thèse de Christophe GUERIN – 1994 – INPG
- « Simulation of induction machine operation using complex magnetodynamic finite elements » de Eric VASSENT – IEEE Transactions on magnetics, vol. 25, No 4, Juillet 1989
Modèles Flux
Les modèles équivalents proposés dans Flux pour la loi de comportement B(H) sont présentés dans le tableau suivant.
| Modèle | Hypothèse | Courbe B(H) équivalente |
|---|---|---|
| Courbe non modifiée | B(H) réelle | |
| Induction sinusoïdale |
B sinusoïdal B = Bmsinωt |
Ce modèle se base sur l'équivalence énergétique suivante :
Ce modèle est plus adapté à une alimentation en tension . |
| Champ H sinusoïdal |
H sinusoïdal H = Hmsinωt |
Ce modèle se base sur l'équivalence énergétique suivante :
Ce modèle est plus adapté à une alimentation en courant . |
| Mixte |
Ce modèle est la combinaison linéaire des deux modèles précédents Beq = αBeqBsin +(1- α )BeqHsin Heq = αHeqBsin +(1- α )HeqHsin où α est un coefficient de pondération choisi de façon empirique ( α doit être compris dans l'intervalle 0,1) |
|
| Moyenne de ν sur une période |
B sinusoïdal B = Bmsinωt |
Ce modèle s'appuie sur une réluctivité équivalente ν eq calculée en faisant la moyenne de la réluctivité sur une période temporelle :
Il est beaucoup moins précis que les autres pour les inductions élevées car il ne respecte pas l'asymptote de pente µ0. |