Spot Weld Fatigue Analysis

Allows for the study of fatigue performance of spot welds in structures.

Currently, only Stress-Life (SN) based Spot Weld Fatigue Analysis is supported. Spot weld fatigue can only be applied to spot welds between two shells. The spot weld location is defined by three attributes, sheet 1, sheet 2, and the nugget. The sheets are defined by shell elements, and the nugget is defined by CWELD, CBAR, CBEAM, or CHEXA elements. The nugget can be directly connected to the shells or RBE2/RBE3 elements can be used to connect the nugget to the shells.

Figure 1. Spot Weld Fatigue

The length of the spot weld is determined by the attached shell thicknesses. If T1 and T2 are the thicknesses of the two shells, then the length of the spot weld element, L is equal to (T1+T2)/2.

Implementation

The simplified representation of a spot weld is used in HyperLife to model the fatigue behavior at the weld.

A single weldment may contain a number of sections welded together with welds of different types. However, in this section you only look at analyzing the sections that contain spot welds. Refer to Seam Weld Fatigue Analysis for details about other weld types.

Simplified Spot Weld Representation

A spot weld is represented as a CBAR, CBEAM, CWELD, or CHEXA elements connected to two sheets of shell elements (PSHELL). The CWELD and CBEAM elements are equivalent to a CBAR element internally. The CHEXA element grid point forces are resolved as beam forces at the geometric centers of each face and then they are considered similar to other 1D elements for fatigue calculations.

Spot Weld Fatigue

Fatigue analysis for spot welds involves examining the weld at three distinct locations, the center planes of the two attachment sheets at the points of attachment and at the center of the nugget and is based on a paper by Rupp et al. The cross-sectional forces and moments at each of the three locations is determined and used to calculate corresponding stresses. These stresses are then used to calculate Fatigue Damage using Rainflow counting and the SN approach.

Figure 2. Spot Weld Fatigue Locations

The following sections illustrates how stresses and subsequently damage are calculated at each of the three locations shown in Figure 3.

Sheet Location (1 or 2)

At sheet location 1 or 2, damage is calculated at the point where the weld is attached to the sheet/shell.

Sheet Location 1

The sheet location 1 is identified by the end A (grid GA) of the nugget (for 1D element nugget) and the face corresponding to the lowest ID’s of the nugget (for CHEXA element nugget). For the structure of CHEXA nugget, refer to Fatigue Input/Output.

Sheet Location 2

The sheet location 2 is identified by the end B (grid GB) of the nugget (for 1D element nugget) and the face corresponding to the highest ID’s of the nugget (for CHEXA element nugget). For the structure of CHEXA nugget, refer to Fatigue Input/Output.

Forces and Moments are generated as output from the applied loading for the weld element (CWELD, CBAR, CBEAM, or CHEXA). As explained previously, the calculation process involves an extra step for CHEXA elements, and except for this difference, the procedure is identical for all spot weld elements. Even though the sheet fatigue behavior point is being examined, the forces at the ends of the weld element are used since they are equivalent.

Figure 3. Forces and Moments of Interest at the Sheet Locations

Radial stresses are calculated at the sheet locations by considering weld element forces at the attachment points. The radial stresses

σ (θ)

are calculated as a function of

θ

for each point in the load-time history as:(1)

σ (θ) = - σ_{\max} (f_{y}) \cos θ - σ_{\max} (f_{z}) \sin θ + σ (f_{x}) + σ_{\max} (m_{y}) \sin θ - σ_{\max} (m_{z}) \cos θ

Where,(2)

σ_{\max} (f_{y}) = \frac{f_{y}}{π D T}

(3)

σ_{\max} (f_{z}) = \frac{f_{z}}{π D T}

$σ (f_{x}) = κ (\frac{1.744 f_{x}}{T^{2}})$ for $f_{x} > 0.0$

σ (f_{x}) = 0.0

for

f_{x} \leq 0.0

(4)

σ_{\max} (m_{y}) = κ (\frac{1.872 m_{y}}{D T^{2}})

(5)

σ_{\max} (m_{z}) = κ (\frac{1.872 m_{z}}{D T^{2}})

Where,

$D$: Diameter of the weld element
$T$: Thickness of the sheet under consideration for damage calculation
$κ$: Calculated as $κ = 0.6 \sqrt{T}$

The equivalent radial stresses are calculated at intervals of $θ$ (Default =18 degrees). The value of $θ$ can be modified by varying the NANGLE field in the Assign Material tool. Subsequently, Rainflow cycle counting is used to calculate fatigue life and damage at each angle ( $θ$ ). The worst damage value is then picked for output. A similar approach is conducted for the other sheet.

Nugget Location

The nugget location is at the center of the weld element. Forces and moments are generated as output from the applied loading for the weld element (CWELD, CBAR, CBEAM, or CHEXA). As explained previously, the calculation process involves an extra step for CHEXA elements, and except for this difference, the procedure is identical for all spot weld elements.

Figure 4. Forces and Moments of Interest at the Nugget Cross-Section

The absolute maximum principal stresses are calculated using the shear stress and bending stress of the beam element as a function of θ for each point in the load-time history as:(6)

τ (θ) = τ_{\max} (f_{y}) \sin θ + τ_{\max} (f_{z}) \cos θ

(7)

σ (θ) = σ (f_{x}) + σ_{\max} (m_{y}) \sin θ - σ_{\max} (m_{z}) \cos θ

Where,(8)

τ_{\max} (f_{y}) = \frac{16 f_{y}}{3 π D^{2}}

(9)

τ_{\max} (f_{z}) = \frac{16 f_{z}}{3 π D^{2}}

$σ (f_{x}) = \frac{4 f_{x}}{π D^{2}}$ for $f_{x} > 0.0$

σ (f_{x}) = 0.0

for

f_{x} \leq 0.0

(10)

σ_{\max} (m_{y}) = \frac{32 m_{y}}{π D^{3}}

(11)

σ_{\max} (m_{z}) = \frac{32 m_{z}}{π D^{3}}

$D$ is the diameter of the weld element.

$T$ is the thickness of the sheet under consideration for damage calculation.

The stresses are calculated at intervals of $θ$ (Default =18 degrees). The value of $θ$ can be modified by varying the NANGLE field in the Assign Material tool. The equivalent maximum absolute principal stresses are calculated for each $θ$ from $τ (θ)$ and $σ (θ)$ . These stresses are used for subsequent fatigue analysis. Rainflow cycle counting is used to calculate fatigue life and damage at each angle ( $θ$ ). The worst damage value is then picked for output. A similar approach is conducted for the other sheet.

Fatigue Input/Output

Fatigue input for Spot Weld Fatigue Analysis can be divided into the following categories:

Fatigue Element Identification

The spot welds (CBAR, CWELD, CBEAM) are referenced with the connected sheets as groups. These groups are currently referenced through components.
The spot weld diameter, which is a function of the minimum shell element thickness, should be input in the Assign Material dialog.
The result file should contain the shell thickness output to be automatically referred to the HyperLife Assign Material tool.
CHEXA elements can be used to define the weld element for Spot Weld Fatigue Analysis. In such cases, the grid point forces are resolved into corresponding forces and moments at the face centers of the opposing faces connected to the shells. The faces of the CHEXA element attached to the sheets should always consist of grid points in the following order.

Figure 5. Faces of the CHEXA that Should be Used as Connection Faces with Shells for Spot Weld Fatigue

Additionally, the default weld element diameter of the CHEXA element for spot weld fatigue is equal to two times the smallest distance from the attachment face centroid to the edges.

Fatigue Parameters (Spot Weld Fatigue Dialog)

The RUPP method is currently applied to calculate the spot weld fatigue analysis.
The spot weld fatigue parameters are applied in this dialog.
Mean stress and thickness corrections are to be activated if the corresponding parameters are to be applied in the Assign Material dialog.
For more information on FKM mean stress correction, see the FKM section under Uniaxial S-N Fatigue.
FE Model units are specified in this dialog. The default unit specified is MPa. Thickness reference will be automatically modified based in the FE model unit selection.

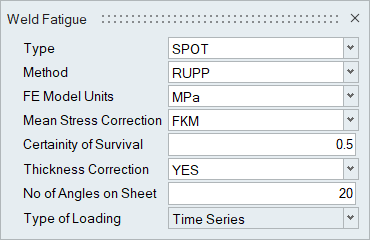
Figure 7.

Fatigue Material

The material properties (SN curve attributes for sheet 1, sheet 2, and the nugget) to be associated with the spot weld group are specified in the Assign Material dialog (SN attributes from the My Material or Material Database tab).
The mean stress sensitivity value and the thickness correction values are specified in the Assign Material dialog.
By default, the shell thickness of the sheets is referenced from the model. The sheets are editable in HyperLife.
The spot weld diameter is to be specified in the Thick/Dia entry in the Assign Material dialog.
TREF is set to 25mm by default, which is equivalent to 1 inch, as specified by the standard.

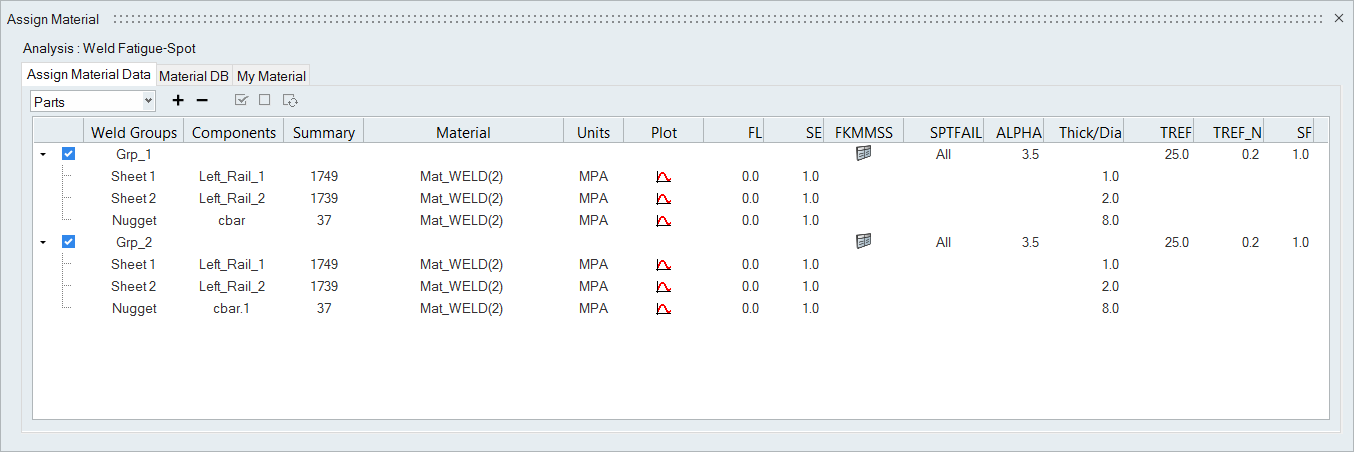
Figure 8.

SPTFAIL

Damage assessment option type

SHEET

Only assess sheet damage at the spot weld location

NUGGET

Only assess nugget damage at the spot weld location

All (Default)

Assess both sheet and nugget damage at the spot weld location

AUTO

Automatically assess damage based on the following conditions, if:

$D < α \sqrt{T}$: Assess nugget damage at the spot weld location
$D \geq α \sqrt{T}$: Assess sheet damage at the spot weld location

Where D is the diameter of the weld connector, α is set using the ALPHA field, and T is the thickness of the shell.

ALPHA

The value of α used to determine the AUTO option on the SPTFAIL field

Default = 3.5 (Real > 0.0)

TREF

Reference thickness for thickness effect consideration

Default = 25.0 (Real > 0.0)

TREF_N

Exponent for the thickness effect consideration

Default = 0.2 (Real ≥ 0.0)

SF

Stress scale factor.

Default = 1.0 (Real > 0.0)

Fatigue Loads

Similar to regular fatigue analysis, the fatigue loads are specified in the Load Map tool.

Output

Output for Spot Weld Fatigue Analysis is provided similar to regular Fatigue Analysis results. Damage and Life results for the SHEET, NUGGET, ALL or Auto are available based on the SPTFAIL selection in the Assign Material dialog. The damage calculation lists the worst damage if Auto is selected.