ACU-T: 7000 Parametric Optimization with AcuSolve
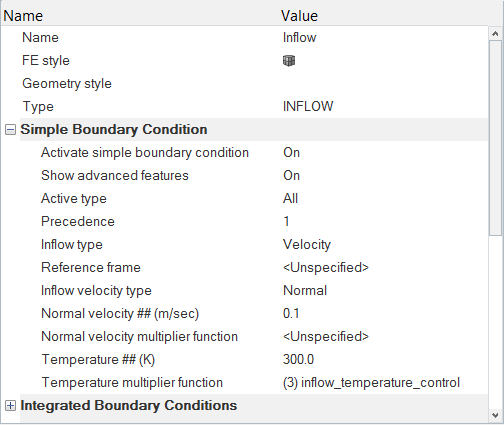
This tutorial provides instructions for setting up, solving, and viewing results for a parametric optimization problem in AcuSolve. The parametric studies enable you to specify one or more conditions that may vary, such as a sweep over a range of inlet mass flow boundary conditions. The range and frequency of the parameter controlling the mass flow is selected either by simply specifying the desired values or having the program compute suitable values automatically. Several parameters can be used in parametric studies, for instance, controlling the inlet mass flow, the impeller rotational speed, and blade angles of a fan problem. The model used for this tutorial consists of a sphere immersed in a fluid flow. The surface of the sphere is kept hot from an internal heat source. The fluid flow removes the heat from the sphere surface, thus causing the temperature of the fluid to rise. The simulation is run with various values of temperature at the fluid inlet to determine the conditions which result in the outlet temperature closest to a desired value.
- Setting up a parametric optimization problem in AcuSolve
- Post-processing a parametric optimization problem
In this tutorial, you will:
- Analyze the problem
- Import the HyperMesh model database
- Set general simulation parameters and solver settings
- Set material model parameters and nodal initial conditions
- Set up the optimization study parameters
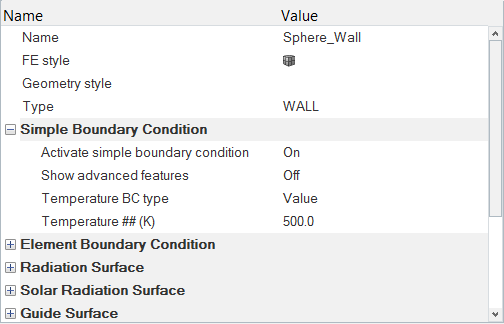
- Assign surface boundary conditions and material properties
- Run HyperMesh
- Monitor the solution with AcuProbe
Prerequisites
Prior to starting this tutorial, you should have already run through the introductory tutorial, ACU-T: 1000 HyperWorks UI Introduction, and have a basic understanding of HyperMesh and AcuSolve. To run this simulation, you will need access to a licensed version of HyperMesh and AcuSolve.
Prior to running through this tutorial, click here to download the tutorial models. Extract ACU-T7000_ParametricOptimization.hm from HyperMesh_tutorial_inputs.zip.
Since the HyperMesh database (.hm file) contains meshed geometry, this tutorial does not include steps related to geometry import and mesh generation.
Analyze the Problem

Figure 1.
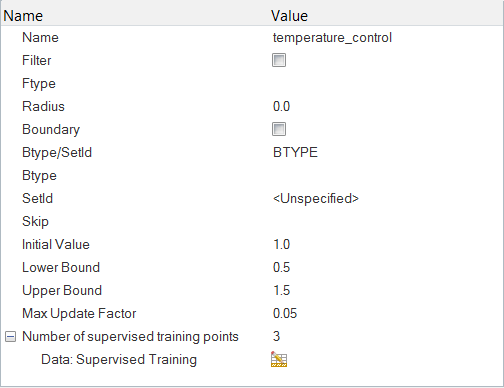
The inlet temperature here is what is known as the “design variable” for the problem. A target value for outlet temperature is specified, and the desired inlet temperature is the value at which the outlet temperature is closest to the target outlet temperature. The difference between the target outlet temperature and the actual outlet temperature is what is known as the “response variable” for the problem. Since the objective of the problem is to minimize the difference between the outlet temperature and the target outlet temperature, this problem is a “minimization” problem.
Optimization
Optimization, in simple terms, is the process of selecting a best input from a set of available alternatives. Almost all engineering problems today are aimed at optimizing something. Airfoil designers are always trying to come up with new airfoil designs with better lift and low drag. Heat exchanger component designers want to maximize the surface heat flux while also minimizing the pressure drop through the exchanger.
HyperMesh offers you two options to setting up an optimization study: design optimization and parametric studies. Design optimization enables you to optimize an objective function subject to certain constraints and satisfaction of flow equations.
Parametric studies enables you to specify one or more conditions that may vary, such as a sweep over a range of inlet mass flow boundary conditions. In parametric studies, these control parameters vary according to a specified pattern. For example, the range and frequency of the parameter controlling the mass flow is selected either by simply specifying the desired values or having the program computing suitable values automatically. Several parameters can be used in parametric studies, for instance, controlling the inlet mass flow, the impeller rotational speed, and blade angles of a fan problem. Perhaps you want to evaluate the pressure rise and torque of the fan; these outputs are called "response variables". The parameters controlling the run conditions are called "variables" or "design variables". The nomenclature is similar to the optimization problems.
- the geometry is allowed to change (geometric design and shape optimization) and/or
- internal parameters, such as the inlet flow rate or viscosity, are allowed to change (design of experiments and quantified optimization).
A minimization problem where a local minimum is sought can be stated as:
Minimize, objective(U,Y)
subject to constraints(U,Y)
Here, U is the flow solution variables and Y is a vector of control parameters, called Design Variables (DVs), that determines the shape of an object or a flow parameter. The objective(s) and constraint(s) are specified by you. A maximization problem is the same as above, but Minimize is replaced with Maximize.
Optimization Solution Sequence
The design optimization may be considered as a sequence of cases, where each case first runs the optimizer and updates the design variables and then solves the flow equations for a number of time steps until convergence. Sample data is gathered at the end of each time step.
- Constructing the response surface from the set of samples.
- Running the optimizer on the response surface.
- Updating the design variables.

Figure 2.
Open the HyperMesh Model Database
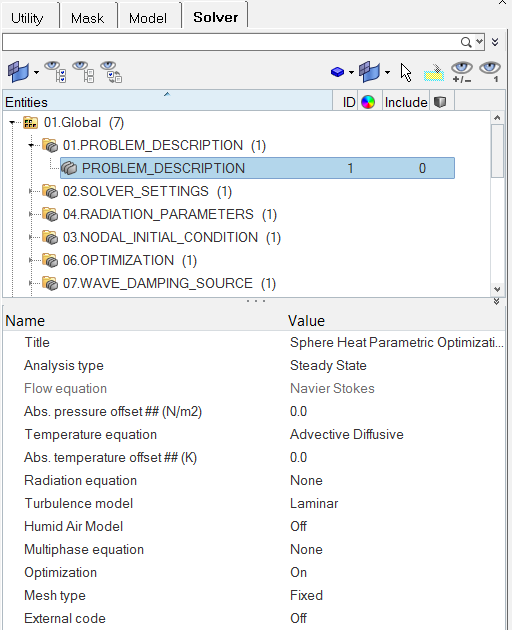
Set the Global Simulation Parameters
Set the Analysis Parameters
In next steps, you will set parameters that apply globally to the simulation.
Specify the Solver Settings
Set Material Model Parameters
In the next steps, you will create a new custom material and assign relevant material properties to it.
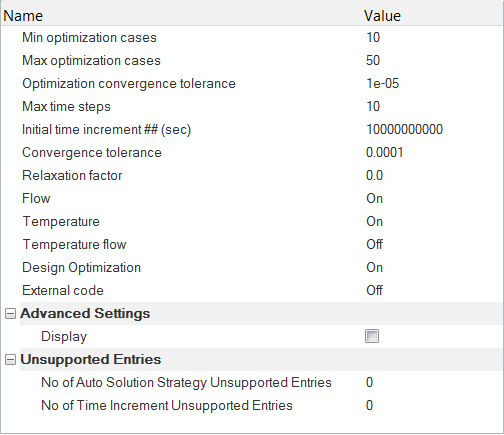
Set Up the Optimization Parameters
Define the Design Variable
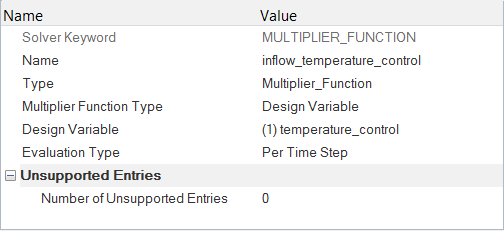
Create a Multiplier Function for the Design Variable
In HyperMesh, multiplier functions are used to scale values of certain parameters at runtime. For example, viscosity of a fluid may vary with temperature. Or inflow rate or temperature may vary over time.
Multiplier functions can also be used to scale the values of the design variables between cases. In quantity optimization, the design variables are linked with the desired quantities in HyperMesh through multiplier functions.
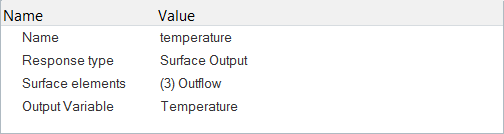
Define Response Variables
Response variables are the building blocks for deriving objective functions and constraints. Examples include: drag, lift, force in an arbitrary direction, total volume, pressure drop, total pressure, uniformity index on temperature, max speed, etc. In other words, response variables are functions of the flow solution (via output mechanism), the design variables, and/or other response variables.
The most basic response variables are functions of the flow solution, extracted from the SURFACE_OUTPUT and ELEMENT_OUTPUT. More complex response variables can be derived from these basic response variables using expressions. An example of this is demonstrated in the following steps.
Define the Objectives
It was mentioned earlier that the response variables are the building blocks for deriving objective functions and constraints. In this section, you will define a new objective and link an existing response variable to that objective entity.
The objective of an optimization problem is usually minimization or maximization of a response variable. In this problem, the objective is to minimize the difference between the actual and the target outflow temperature. In the next few steps, you will create and define the objective accordingly.
Set Up Optimization Controls
In the Optimization command, you will link all the defined objectives and constraints to define the optimization problem. There are no constraints defined for this problem, but if there are any, they should be defined first under the Constraints entry in the Data Tree.
- In the Solver Browser, expand 01.Global then click on 06.OPTIMIZATION.
- In the Entity Editor, verify that the Objective is set to find_inflow_temperature.
- If there are any constraints in your problem, you can set the value for the Number of Constraints field accordingly and then define the constraints.
- Verify that the Optimizer convergence tolerance is set to 1e-4.
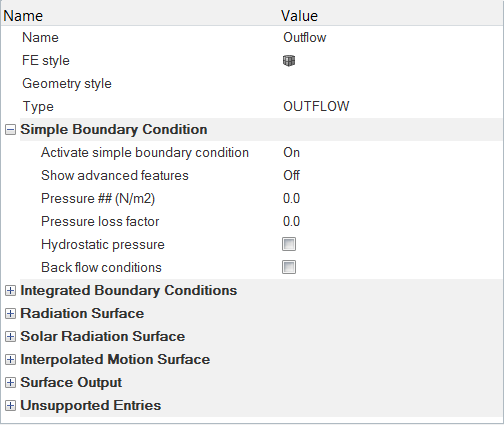
Assign Boundary Conditions and Material Properties
Compute the Solution and Review the Results
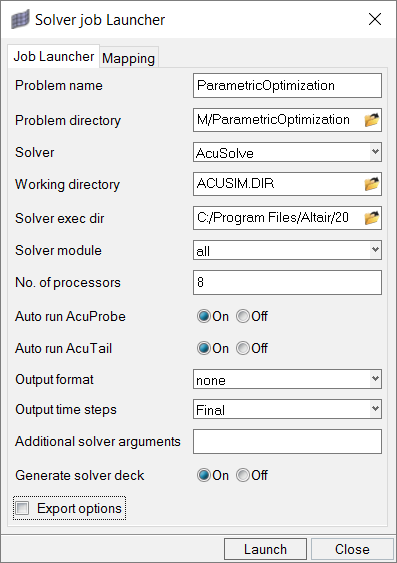
Run HyperMesh
In this step, you will launch AcuSolve directly from HyperMesh and compute the solution.
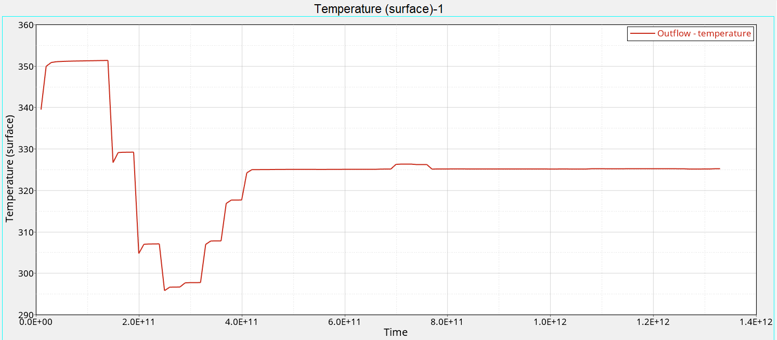
Monitor the Solution with HyperGraph
AcuGetDv and AcuGetRsp
AcuSolve provides two post-processing utilities specific to optimization problems, AcuGetDv and AcuGetRsp. AcuGetDv provides the values of the design variables for all the cases included in the solution. AcuGetRsp provides the values of the response variables for all the cases included in the solution.
Summary
In this AcuSolve tutorial, you successfully set up and solved a parametric optimization problem with AcuSolve. You started the tutorial by creating a database in HyperMesh, importing and meshing the geometry, and setting up the simulation parameters. You defined the design variables, the response variables, and set up the objectives of the problem using the response variables. Once the case was setup, the solution was generated with AcuSolve. HyperGraph was used to visualize the variation of design variables and response variables as the solution progressed through the different cases provided to AcuSolve by the optimization program. You also used the utilities provided in AcuSolve to get the design variables and response variables information for all the cases.