ACU-T:3000 囲まれた温かい円筒:自然対流
前提条件
このチュートリアルでは、熱源を備えた同心円筒の円環内で自然対流によって生じる空気の流れのCFDシミュレーションを設定および解析して、その結果を表示するための手順を説明します。このチュートリアルを開始する前に、HyperWorks 入門チュートリアルである ACU-T:1000 HyperWorksユーザーインターフェースをすでに完了し、HyperMesh、AcuSolve、およびHyperViewの基本を理解しているものとします。このシミュレーションを実行するには、ライセンス供与済みバージョンのHyperMeshおよびAcuSolveにアクセスできる必要があります。
このチュートリアルを実行する前に、ここをクリックしてチュートリアルモデルをダウンロードしてください。 ACU-T3000_HotCylinder.hm をHyperMesh_tutorial_inputs.zipから抽出します。
HyperMeshデータベース(.hmファイル)には、メッシュ済みのジオメトリが含まれているため、このチュートリアルには、ジオメトリのインポートとメッシュ生成に関する手順は含まれません。
問題の説明

図 1.
ここで解析する問題の概略図を上図に示します。内側の円筒は内部発熱を伴うソリッドであり、内側と外側の円筒間の円環スペースは、流体として空気が入っている流体ボリュームです。内側円筒のサーフェスと接触している空気は加熱され、浮力効果によって円環の上部まで上昇して、上部にある冷たい流体を押しのけます。同時に、熱いサーフェスと接触していた流体が周囲の冷たい流体と入れ替わります。定常状態に達するまで、このプロセスが継続的に繰り返されます。両方の円筒は無限に長いものとみなされ、半対称性と周期性を使用してモデル化されています。
円筒はz方向に無限なため、この方向に沿って周期性が適用されます。円筒はz方向に無限なため、この方向に沿って周期性が適用されます。
理論の概要
自然対流
対流は、物質の運動を通して熱エネルギーの移動が起きる熱伝達メカニズムです。対流の定義には物質の運動が含まれるため、対流には、通常流体状態が存在します。この種の熱伝達の多くは、温かいまたは冷たいサーフェスと流体の間で発生します。サーフェスと接触している流体の膜がサーフェスから熱を吸収したり、サーフェスに熱を伝達したりして、新しい膜に置換されます。この流体の運動は、ファンやポンプなどの外部ソースによって制御される場合もあれば、流体特性の内部変化が原因で発生する場合もあります。外部ソースが流体運動の原因ではない場合、作用している熱伝達メカニズムは自然対流と呼ばれます。自然対流における流体の運動の原動力は、熱伝達によって流体内で引き起こされる温度勾配による流体の密度変化です。
自然対流メカニズムは、前述の問題の説明と同様に機能します。サーフェスと接触している流体は、サーフェスから熱を吸収したり、サーフェスに熱を伝達したりして、周囲の流体よりも温かくなったり、冷たくなったりします。温度勾配によって引き起こされる密度差から生じる浮力によって、流体は上下に移動します。流体が移動してできた空隙を周囲の流体が満たし、同じプロセスが繰り返されます。これにより、温かい流体を対流セルの一番上に、冷たい流体を一番下に運ぶ対流が発生します。浮力効果は重力によって引き起こされるため、自然対流が起きるためには重力の存在が不可欠です。ただし、重力は流体運動の背後にある原動力ではないことに注意する必要があります。重力の存在は、温度勾配によって引き起こされる密度変化から生じる流体の移動を可能にするだけです。
自然対流の始まりは、レイリー数(Ra)と呼ばれる無次元数によって数学的に特定されます。レイリー数は次のように定義されます。
- xは特性長さ(m)
- は特性長さxのレイリー数
- は重力加速度(m/s2)
- はサーフェス温度(K)
- は静止温度(物体のサーフェスから遠く離れた流体の温度)(K)
- は動粘性率(m2/s)
- αは熱拡散率(m2/s)
- βは熱膨張係数(絶対温度の理想気体の場合)。
流体特性、α、およびβは膜温度、、以下のように定義されます:
レイリー数が流体の臨界値を下回っている場合、熱伝達は主に伝導の形態を取ります。この臨界値を上回っている場合、主な熱伝達メカニズムは対流になります。
ブシネスク密度モデル
ブシネスク密度モデルは、自然対流などの浮力流れに適用される近似法です。ブシネスク近似では、重力加速度。この近似の基本は、温度変化が小さいために結果的に密度の変化も小さくなり、無視できるということです。ただし、で乗算した場合は、結果の項が無視できない力にまで増大します。ブシネスク近似は次のようになります。
- は温度
- は基準温度(における密度(kg/m3)
- は温度(K)
近似で説明したように、ブシネスク密度モデルは、密度変化が小さい場合にのみ適用されます。一般的な指針は、条件が真であることを確認することです。これにより、流体内部の想定温度差が大きくないケースにのみ使用するという制限が間接的にこのモデルに加えられます。
HyperMeshモデルデータベースを開く
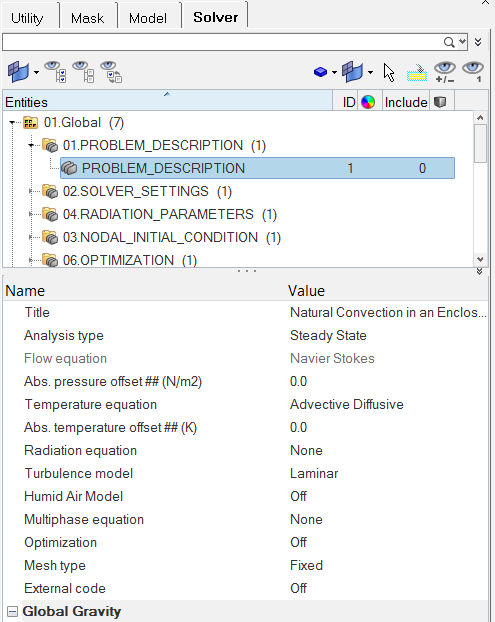
一般的なシミュレーションパラメータの設定
一般的なシミュレーションパラメータの設定
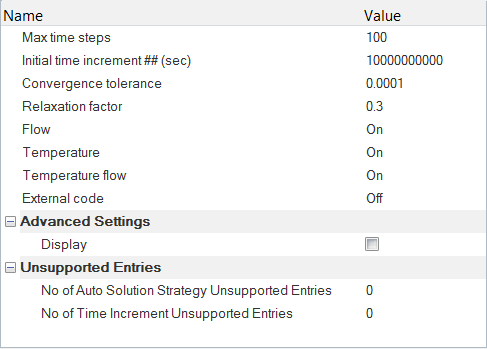
ソルバー設定
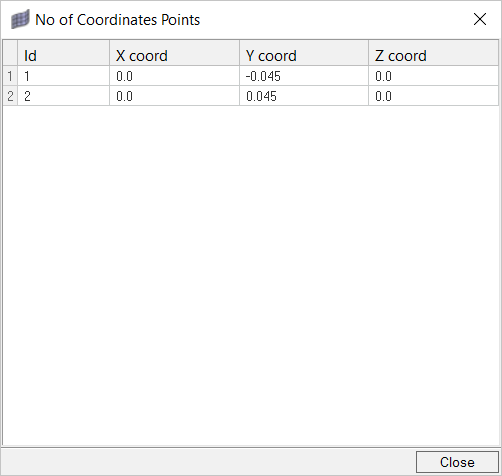
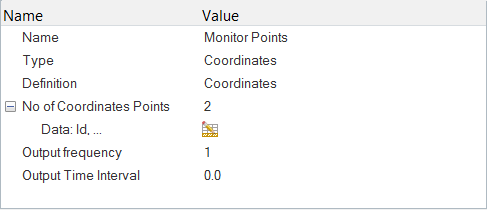
時刻歴出力ポイントの作成
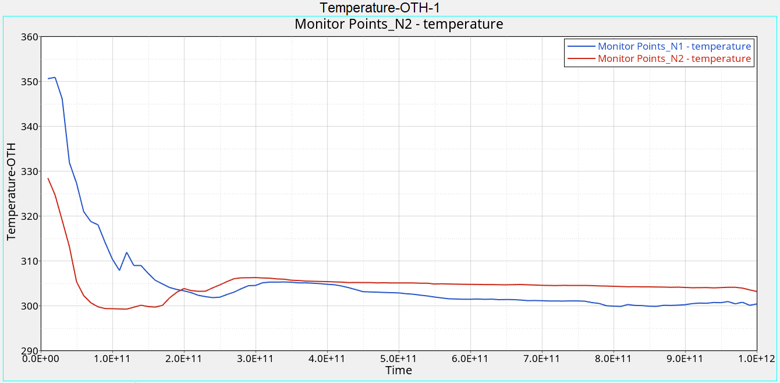
Time History Outputコマンドを使用すれば、領域内の任意の点の節点解を抽出することができます。
物体力と材料モデルパラメータの設定
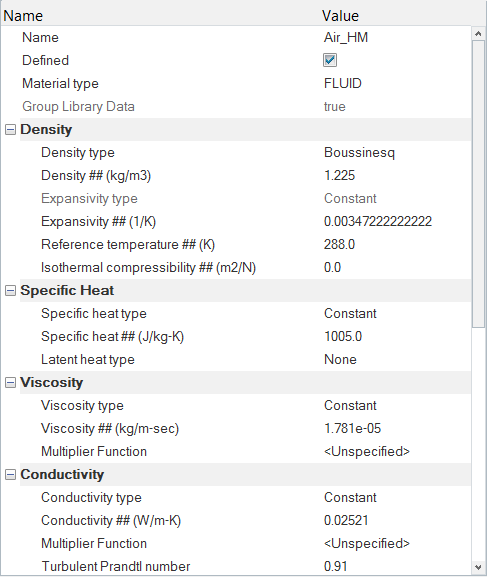
空気の材料モデルパラメータの変更
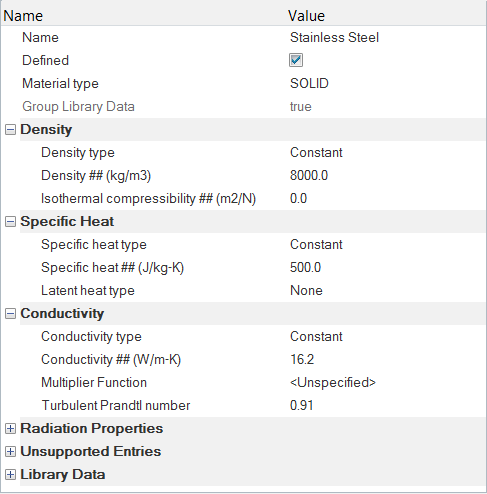
ソリッドの材料モデルの作成
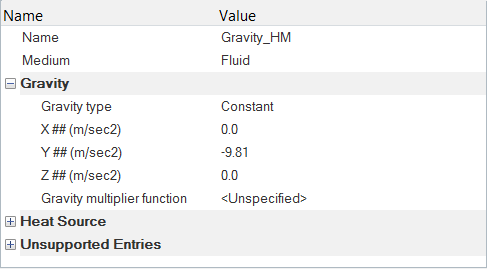
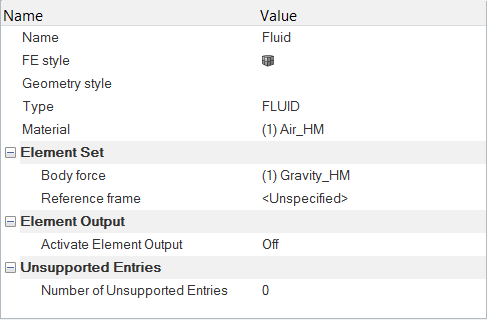
重力物体力の定義
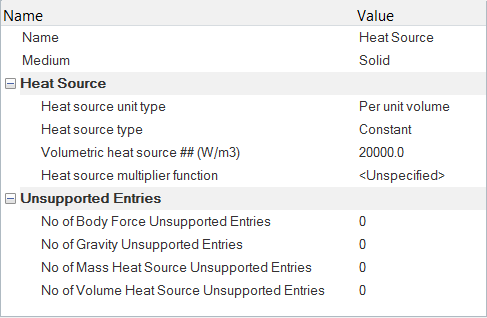
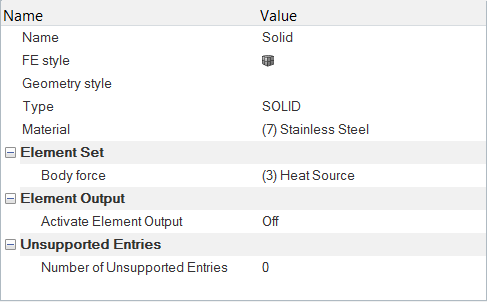
体積熱源の定義
境界条件と初期状態の設定
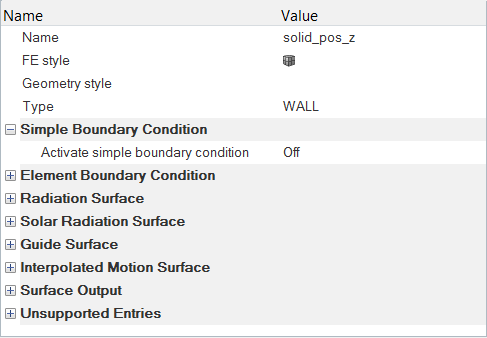
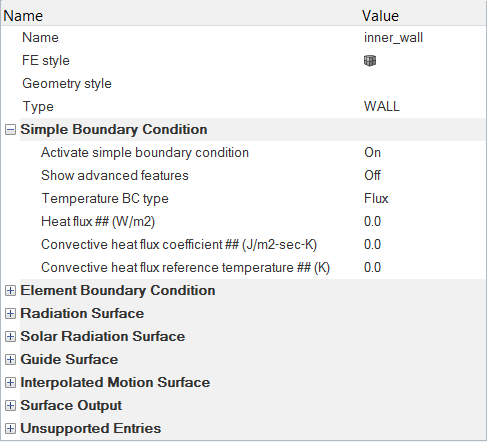
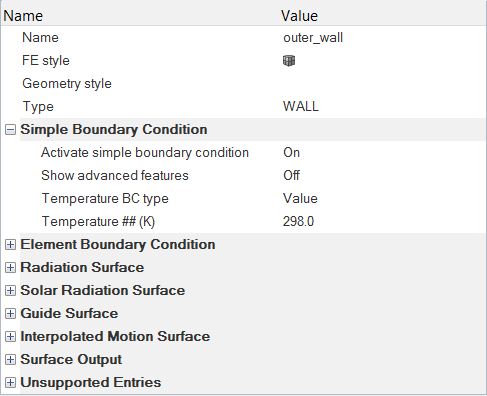
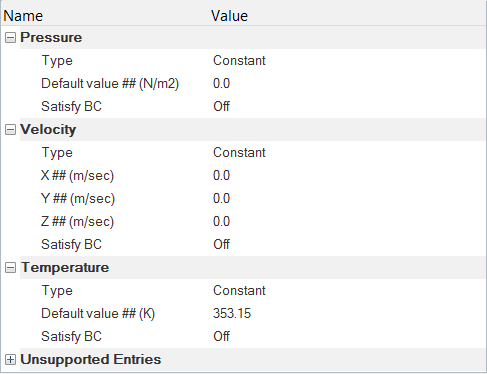
材料特性とサーフェス境界条件の設定
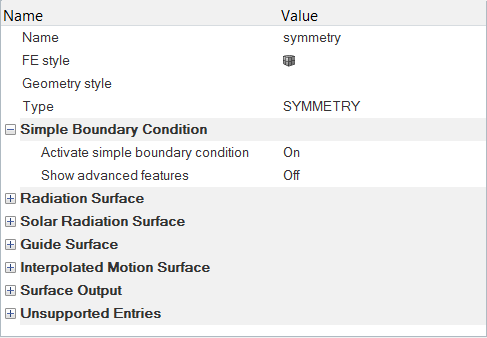
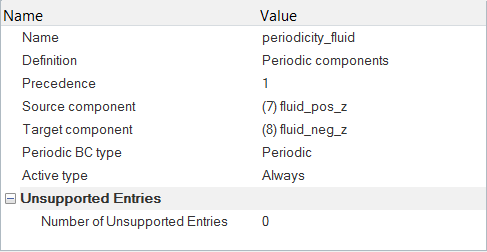
周期境界条件の指定
無限に長い領域の一部のみをモデル化しているため、周期的境界条件を指定することで、解析の周期性を設定する必要があります。その結果として、解析は周期性によって制約されます。周期的境界条件によって、周期性が定義されている2つのサーフェス上の対応する節点のペア同士がリンクされます。
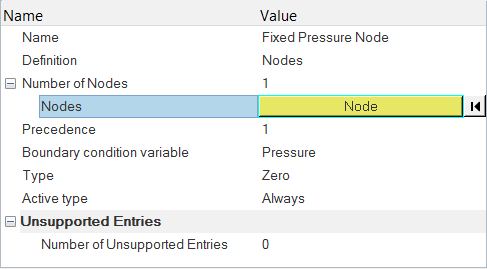
基準圧力の設定
このモデルのセットアップには入口と出口は含まれていないため、基準圧力を手動で指定する必要があります。このためには、流体領域内の任意の節点で圧力節点境界条件を指定します。
節点初期状態の指定
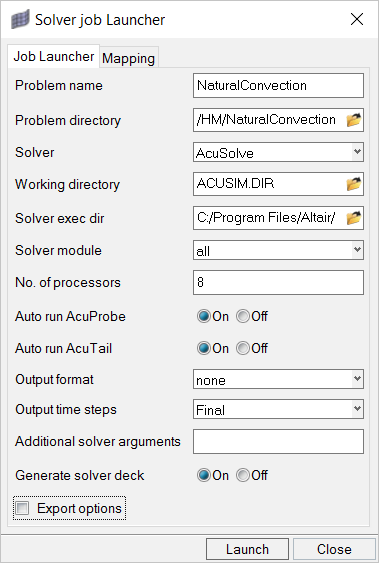
解析計算
HyperGraphによる結果のポスト処理
HyperViewによる結果のポスト処理
HyperViewのオープンとモデルおよび結果の読み込み
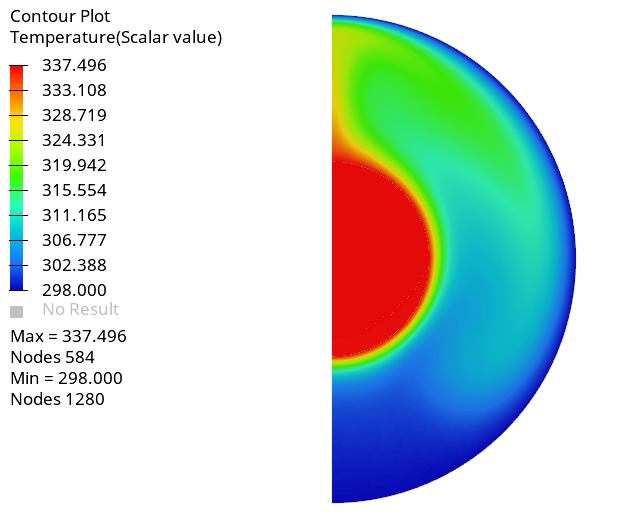
温度分布コンターの作成
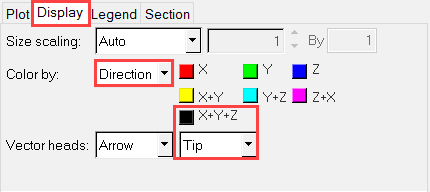
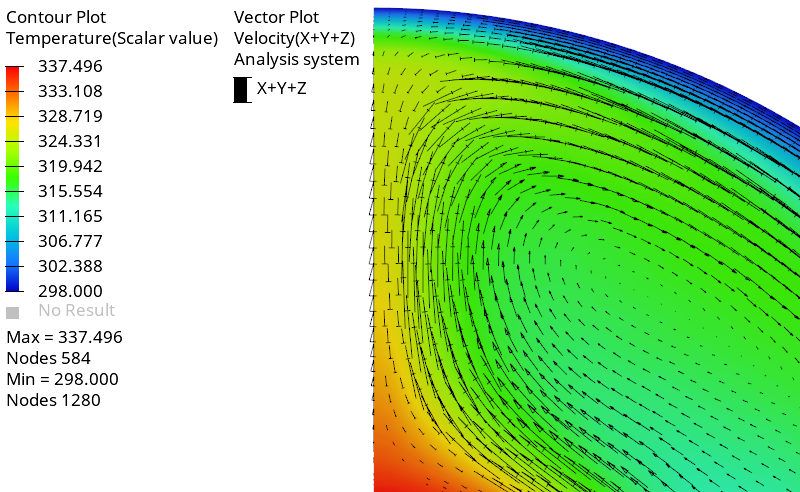
速度ベクトルプロットの作成
要約
このチュートリアルでは、AcuSolveとHyperMeshを使用して自然対流問題を正しく設定し、解析する方法を知ることができました。まずHyperMeshモデルデータベースをインポートし、シミュレーションパラメータと境界条件を設定しました。解が計算された後に、HyperViewを使用して結果をポスト処理し、領域全体にわたる温度分布のコンタープロットを作成しました。

 をクリックすることで、xy平面を正面から見た表示にします。
をクリックすることで、xy平面を正面から見た表示にします。