ACU-T:7000 AcuSolveによるパラメトリック最適化
このチュートリアルでは、AcuSolveでのパラメトリック最適化問題の設定、解析、および結果表示を行うための手順を説明します。パラメトリックスタディでは、一定範囲の入口質量流量境界条件のスイープなど、変化する可能性のある1つまたは複数の条件を指定できます。質量流量を制御するパラメータの範囲および周波数は、ただ目的の値を指定するか、プログラムに適した値を自動計算させることによって選択されます。パラメトリックスタディでは、いくつかのパラメータを使用して、たとえばファン問題の入口質量流量、羽根車の回転速度、羽根角などを制御できます。このチュートリアルで使用されるモデルは、流体の流れにさらされる1つの球で構成されます。この球のサーフェスは、内部熱源によって高温に保たれています。流体の流れによって球のサーフェスから熱が奪われ、その結果、流体の温度が上昇します。流体の入口にさまざまな温度値を設定してシミュレーションを実行することで、出口温度が目標値に最も近くなる条件を特定します。
- AcuSolveでのパラメトリック最適化問題の設定
- パラメトリック最適化問題のポスト処理
このチュートリアルでは、以下を実行します。
- 問題の解析
- HyperMeshモデルデータベースのインポート
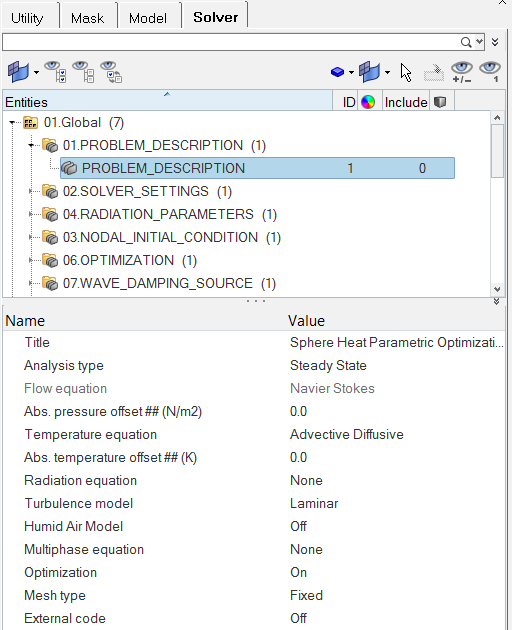
- 一般的なシミュレーションパラメーターとソルバーの設定
- 材料モデルパラメータと節点初期条件の設定
- 最適化スタディのパラメータの設定
- 境界条件と材料特性の割り当て
- AcuSolveの実行
- AcuProbeによる解析のモニター
前提条件
このチュートリアルを開始する前に、HyperWorks 入門チュートリアルである ACU-T:1000 HyperWorksユーザーインターフェースをすでに完了し、HyperMeshとAcuSolveの基本を理解しているものとします。このシミュレーションを実行するには、ライセンス供与済みバージョンのHyperMeshおよびAcuSolveにアクセスできる必要があります。
このチュートリアルを実行する前に、ここをクリックしてチュートリアルモデルをダウンロードしてください。 ACU-T7000_ParametricOptimization.hm をHyperMesh_tutorial_inputs.zipから抽出します。
HyperMeshデータベース(.hmファイル)には、メッシュ済みのジオメトリが含まれているため、このチュートリアルには、ジオメトリのインポートとメッシュ生成に関する手順は含まれません。
問題の解析

図 1.
ここで入口温度は、この問題の“設計変数”と呼ばれるものです。出口温度の目標値が指定されており、望ましい入口温度は、出口温度がこの目標出口温度に最も近くなる値となります。目標の出口温度と実際の出口温度の差は、この問題の“応答変数”と呼ばれるものです。この問題の目的は、実際の出口温度と目標の出口温度の差を最小化することであるため、この問題は“最小化”問題です。
最適化
最適化とは、簡単に言うと、一連の選択肢の中から最適な入力を選択するプロセスです。今日のほとんどすべての工学的問題は、何かを最適化することを目的としています。航空機の翼の設計者は常に、揚力に優れ、抗力の低い新しい翼を設計しようと努めています。熱交換器部品の設計者は、表面熱流束を最大化する一方で、交換器を通じた圧力低下を最小限に抑えることを目指しています。
AcuSolveは、最適化の調査を設定するための2つの手法として、設計最適化とパラメトリックスタディを提供します。設計最適化によって、特定の制約を受け、流動方程式を満たすことを条件とする目的関数を最適化できます。
パラメトリックスタディでは、一定範囲の入口質量流量境界条件のスイープなど、変化する可能性のある1つまたは複数の条件を指定できます。パラメトリックスタディにおいて、これらの制御パラメータは指定されたパターンに従って変化します。たとえば、質量流量を制御するパラメータの範囲および周波数は、ただ目的の値を指定するか、プログラムに適した値を自動計算させることによって選択されます。パラメトリックスタディでは、いくつかのパラメータを使用して、たとえばファン問題の入口質量流量、羽根車の回転速度、羽根角などを制御できます。おそらく、希望される評価対象はファンのトルクと圧力上昇でしょう。これらの出力は“応答変数”と呼ばれます。実行条件を制御するパラメータは、“変数”または“設計変数”と呼ばれます。この呼称は、最適化問題の場合と同様です。
- 形状は変化することが許容される(形状設計および形状最適化)
- 入口の流速や粘度などの内部パラメータは変化することが許容される(実験計画法および定量化された最適化)
局所最小値を求める最小化問題は、次のように表現できます。
最小化, 目的(U,Y)
条件 制約(U,Y)
ここで、Uは流れ解析変数、Yは設計変数(DV)と呼ばれる、オブジェクトの形状または流れパラメータを決定する制御パラメータのベクトルです。目的と制約は、ユーザーによって指定されます。最大化問題も上記と同様で、最小化が最大化に置き換えられるだけです。
最適化解析の流れ
設計最適化は、連続したケースとみなすことができます。その各ケースでは、まず最適化機能が実行され、設計変数が更新されてから、収束にいたるまでいくつかの時間ステップにわたって流動方程式が解かれます。各時間ステップの終了時にサンプルデータが収集されます。
- サンプルのセットから応答サーフェスを構築します。
- 応答サーフェスに対して最適化機能を実行します。
- 設計変数を更新します。
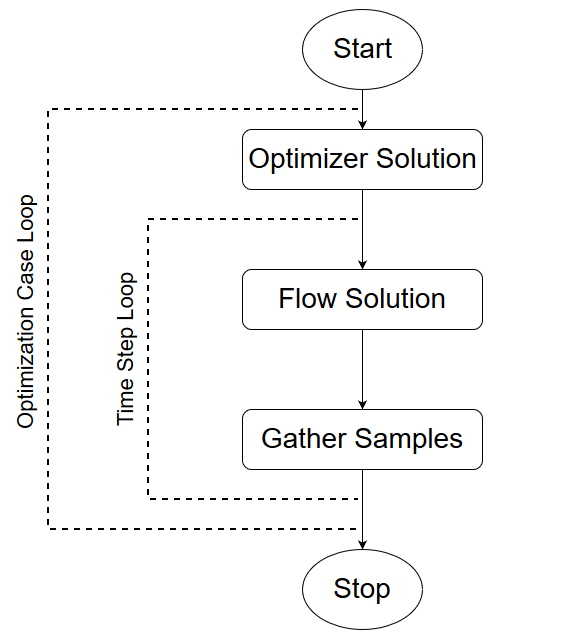
図 2.
HyperMeshモデルデータベースを開く
グローバルなシミュレーションパラメータの設定
解析パラメータの設定
次の手順では、シミュレーション全体に適用されるパラメータを設定します。
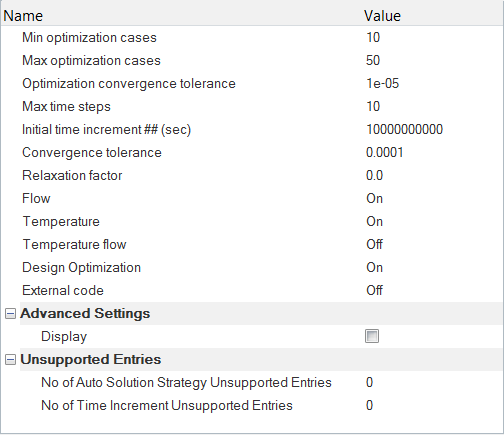
ソルバー設定
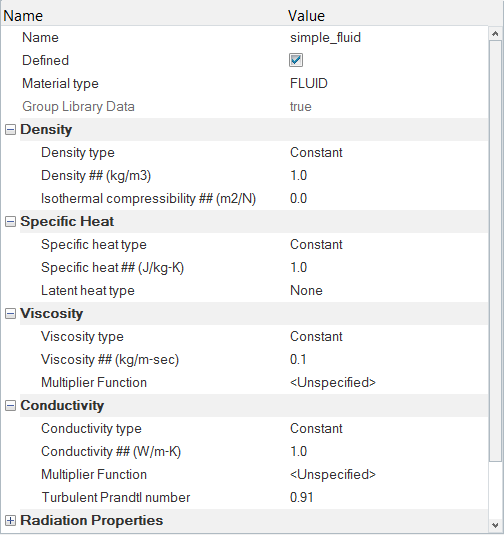
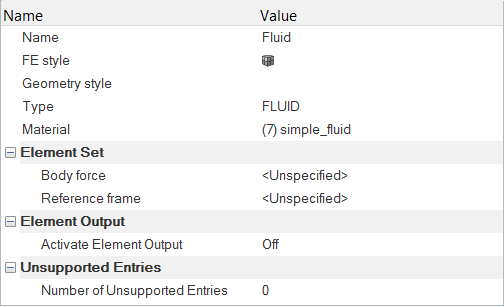
材料モデルパラメータの設定
次の手順では、新しいカスタム材料を作成し、関連する材料特性を割り当てます。
最適化パラメータの設定
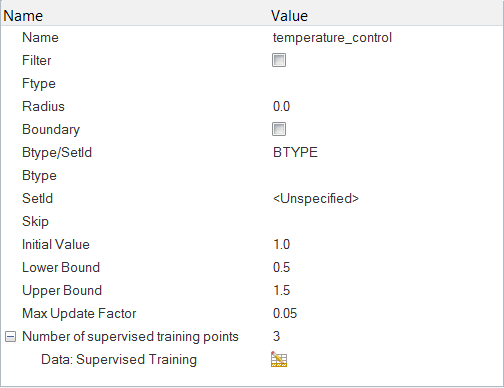
設計変数の定義
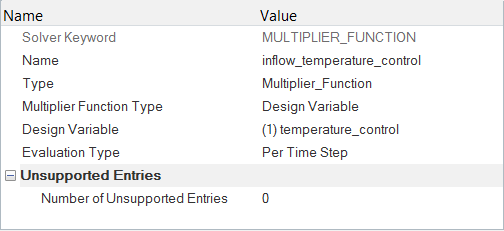
設計変数のMultiplier Functionの作成
AcuSolveでは、実行時にMultiplier Functionを使用して特定のパラメータの値をスケーリングします。たとえば、流体の粘度は温度に応じて変化することがあります。また、流入速度や流入温度は時間とともに変化することがあります。
Multiplier Functionを使用して、ケースごとに設計変数の値をスケーリングすることもできます。数量最適化では、設計変数は、Multiplier FunctionによりAcuSolve内で希望の数量とリンクされます。
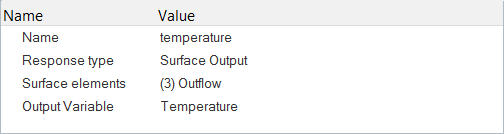
応答変数の定義
応答変数は、目的関数と制約を導出するためのビルディングブロックです。たとえば、抗力、揚力、任意の方向の力、総体積、圧力低下、総圧力、温度の均一性指数、最大速度などが含まれます。つまり、応答変数は、(出力メカニズムを介した)流れ解析の関数、設計変数などとなります。
ほとんどの基本応答変数は、SURFACE_OUTPUTおよびELEMENT_OUTPUTから抽出された流れ解析の関数です。さらに複雑な応答変数は、式を使用してこれらの基本応答変数から導出できます。この例を以下の手順で示します。
目的関数の定義
以前、応答変数は、目的関数と制約を導出するためのビルディングブロックであると説明しました。ここでは、新しい目的を定義し、既存の応答変数をその目的エンティティにリンクさせます。
最適化問題の目的は、通常応答変数の最小化または最大化となります。この問題では、目的は、実際の出口温度と目標の出口温度の差を最小化することです。次の手順では、適宜目的を作成および定義します。
最適化コントロールの設定
最適化コマンドで、定義した目的と制約をすべてリンクし、最適化問題を定義します。この問題では定義されている制約はありませんが、存在する場合は、データツリーのConstraintsエントリの下で最初に定義する必要があります。
- Solverブラウザで01.Globalを展開して06.OPTIMIZATIONをクリックします。
- エンティティエディターで、Objectiveがfind_inflow_temperatureに設定されていることを確認します。
- 問題に制約がある場合は、適宜Number of Constraints欄に値を設定し、その制約を定義できます。
- Optimizer convergence toleranceが1e-4に設定されていることを確認します。
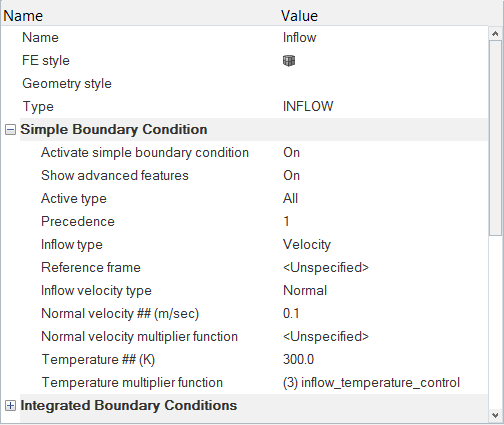
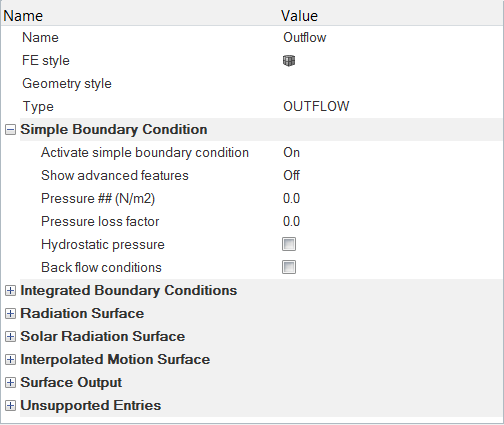
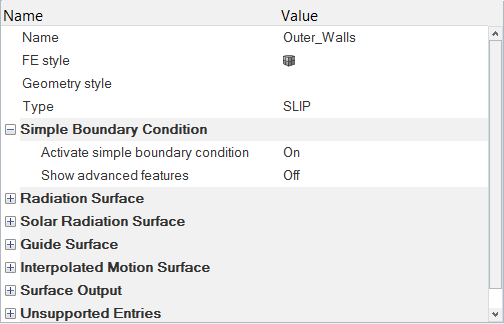
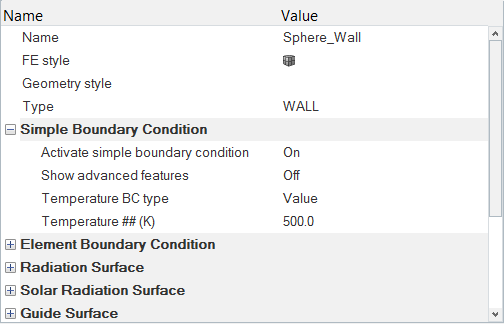
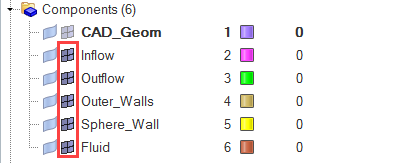
境界条件と材料特性の割り当て
解析と結果の確認
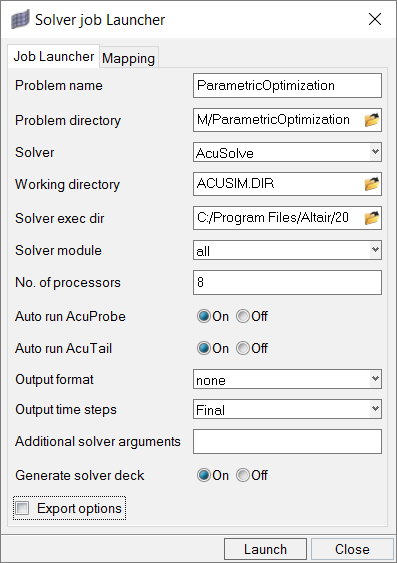
AcuSolveの実行
この手順では、HyperMeshからAcuSolveを直接起動して解析を完了します。
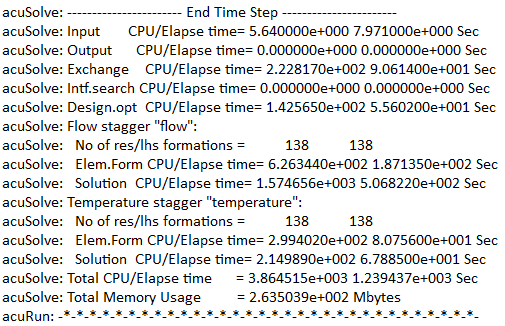
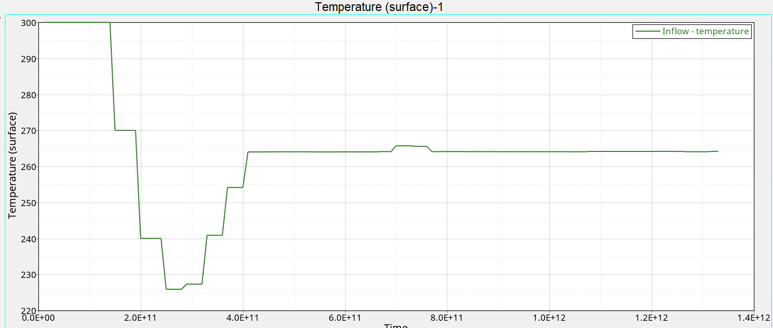
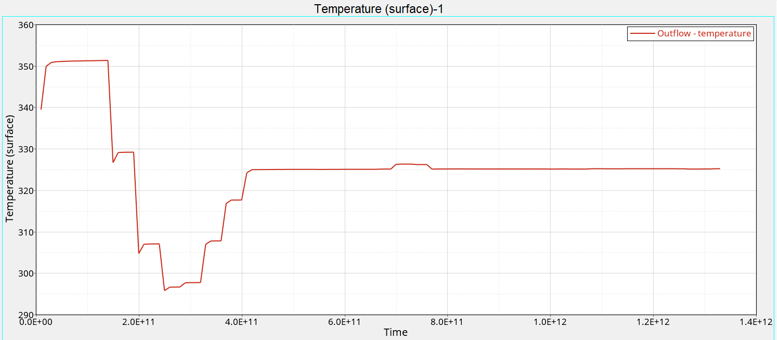
HyperGraphによる解析のモニター
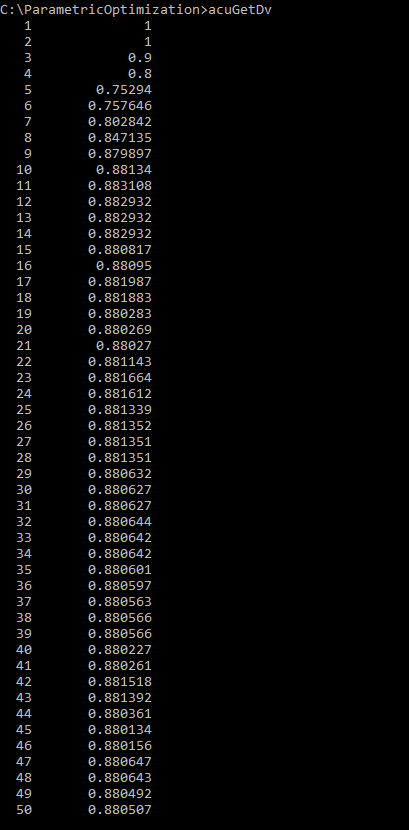
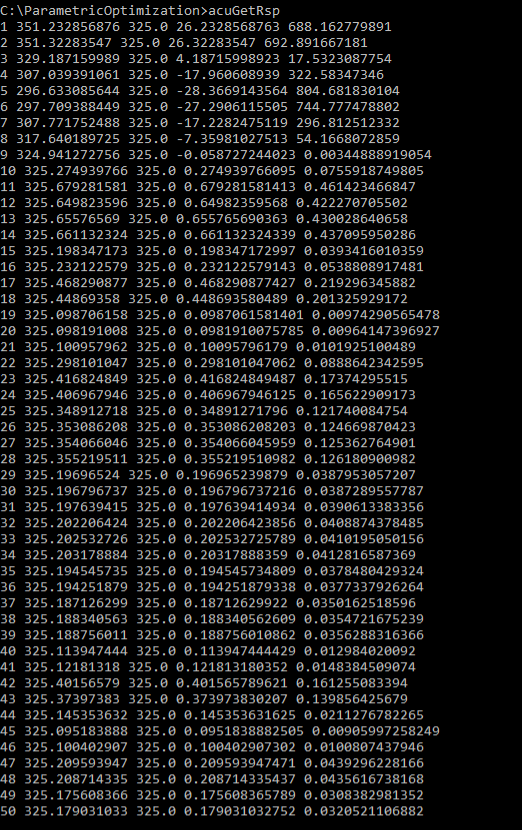
AcuGetDvとAcuGetRsp
AcuSolveでは、最適化問題に固有の2つのポスト処理ユーティリティ、AcuGetDvおよびAcuGetRspを用意しています。AcuGetDvは、解析に含まれるすべてのケースの設計変数の値を提供します。AcuGetRspは、解析に含まれるすべてのケースの応答変数の値を提供します。
要約
このAcuSolveチュートリアルでは、AcuSolveを使用して、パラメトリック最適化問題を正しく設定し、解析しました。チュートリアルは、HyperMeshでデータベースを作成し、形状をインポートしてメッシュ処理し、シミュレーションパラメータを設定することから始めました。設計変数および応答変数を定義し、その応答変数を使用して問題の目的を設定しました。ケースが設定されると、AcuSolveを使用して解が生成されました。最適化プログラムによってAcuSolveに提供されたさまざまなケースで解析が進行する際に、HyperGraphを使用して、設計変数と応答変数が変化する様子を可視化しました。すべてのケースで設計変数および応答変数の情報を取得するため、AcuSolveで提供されているユーティリティも使用しました。