OS-V: 0385 Simply-Supported Thick Square Plate Transient Forced Vibration Response

Test 21T OptiStruct is used to investigate the Peak Displacement in z-direction, the time at the peak displacement, extreme fiber bending stress at undamped Natural Frequency and the Static displacement at the center of the plate.



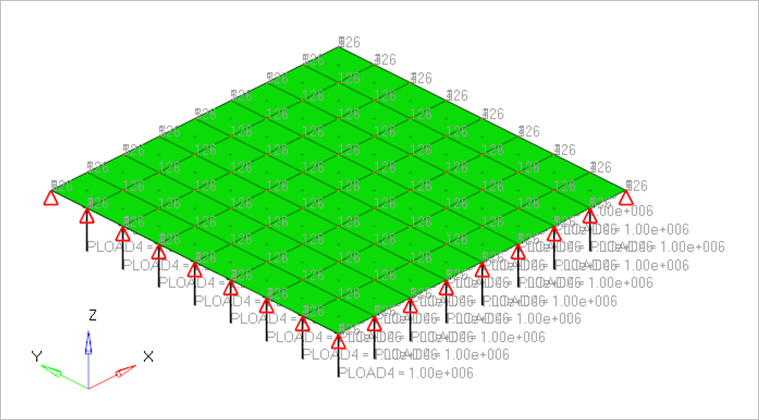
図 1. FE Model with Boundary Conditions and Loadcases

Benchmark Model

The 2nd order and 1st order quad elements are used to model the square plate of thickness 1.0m. The z-rotation and x, y translations are fixed for all the nodes, z-translation is fixed along all four edges, x-rotation is fixed along the edge x=0 and x=10 and y-rotation is fixed along the edge y=0 and y=10. A suddenly applied step load F0=106 N/m2 is induced in the z-direction. For modal analysis solution, a damping ratio of 0.02 is applied in all 16 modes at a time step of 0.0001 secs and for direct solution, Rayleigh damping factor α1=5.772 and α2=6.929×10-5 at a time step of 0.0001 secs are given.

The material properties are:
Material Properties
Value
Young’s Modulus
200 × 109 N/m2
Poisson’s Ratio
0.3
Density
8000 kg/m3

Frequency Response Summary

The frequency of each targeted mode is normalized with the closed form solution.
f*
Closed form solution
  Peak Displacement (mm) Time at Peak Displacement (sec) Peak Stress (N/mm2) Static Displacement (mm)
Reference Solution 4.524 0.0108 62.11 2.333
HOE:        
Direct Solution 4.838 0.011 72.67 2.42
Normalized 0.935097148 0.981818182 0.854685565 0.964049587
Modal Solution 4.870 0.011 75.16 2.42
Normalized 0.928952772 0.981818182 0.82637041 0.964049587
LOE:        
Direct Solution 4.604 0.0108 57.98 2.34
Normalized 0.982623805 1 1.071231459 0.997008547
Modal Solution 4.611 0.0107 58.44 2.341
Normalized 0.981132075 1.009345794 1.062799452 0.996582657

Model Files

必要なモデルファイルのダウンロードについては、モデルファイルへのアクセスを参照してください。

The model files used in this problem include:
  • Test21THOED.fem
  • Test21THOEM.fem
  • Test21TLOED.fem
  • Test21TLOEM.fem

Reference

NAFEMS R0016 - Selected Benchmarks for Forced Vibration, J Maguire, D J, Dawswell, L Gould 1989