MV-3020: Optimize a Two Spring Mass System
In this tutorial you will learn how to setup an optimization problem using MotionSolve’s Optimization Wizard.
MotionSolve is commonly used for performing system level simulation. Simulations are commonly performed to understand how well a specific design performs. Often a goal for such simulations is to find the right set of design parameters that permit the system to perform its intended functions in some optimal way.
Commonly used design variables are the location and orientation of various connectors and their force characteristics. Occasionally the mass and material properties of some bodies are also included as design variables. The system behavior is normally characterized with a set of response variables. So, the goal of simulations often is to find the values of these design variables such that the response variables attain a desired set of values.
In the past such analysis has been done using techniques such as Monte Carlo simulations and design of experiments. These methods work quite well, but they are computationally intensive and require large sets of simulations.
MotionSolve now supports a capability for analytically computing design sensitivities. Design sensitivity is the matrix of partial derivatives of the response variables with respect to the design variables. A gradient-based optimizer is capable of using these sensitivities to minimize a cost function. This process is known as design optimization. A new optimization toolkit that permits optimization of some design problems is also now available in MotionSolve.
Though not as general as the statistical methods, optimization with design sensitivity is significantly faster and is the preferred solution in many instances.
- Process of Optimization with MotionSolve
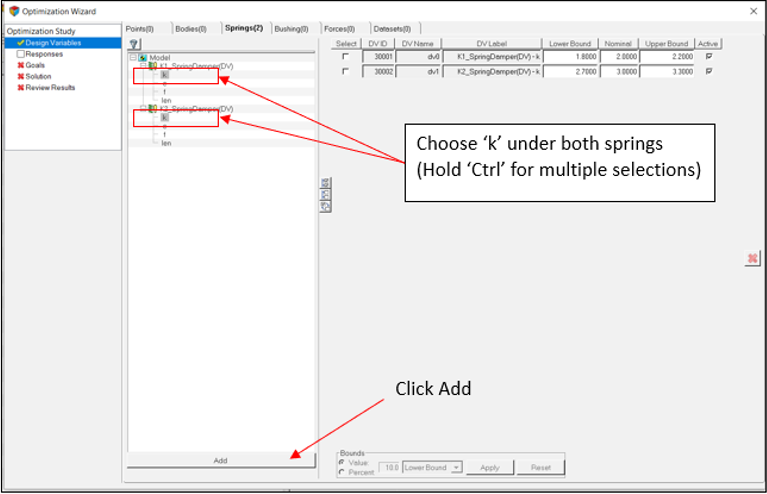
- Defining spring stiffnesses as design variables
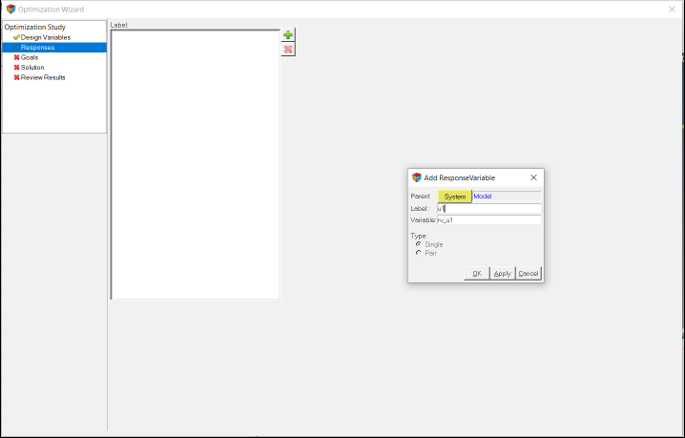
- Defining displacements as responses
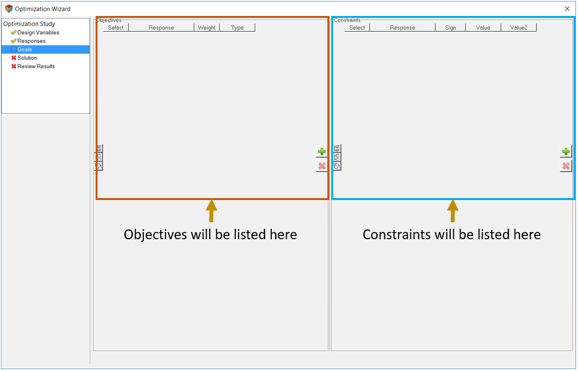
- Using the responses as objectives
- Running the optimization and post-processing the results
- Introduction
-
Two springs are connected in series. The stiffness of spring-1 is k1 and that of spring-2 is k2. One end of spring-1 is fixed to ground while a force, P1, acts at the other end. Spring-2 is subjected to a force of P2 at the other end.
The objective of the analysis is to determine the sensitivities of stiffnesses of the springs to displacements u1 and u2 and use them to identify or tune k1 and k2 of the system to achieve specific values of u1 and u2.
MotionSolve's DSA (Design Sensitivity Analysis) capability to calculate sensitivities is utilized in this example. A Step-by-step procedure to define and run the model is given in the tutorial.
Figure 1 shows that problem setup. Properties used in the problem are also provided.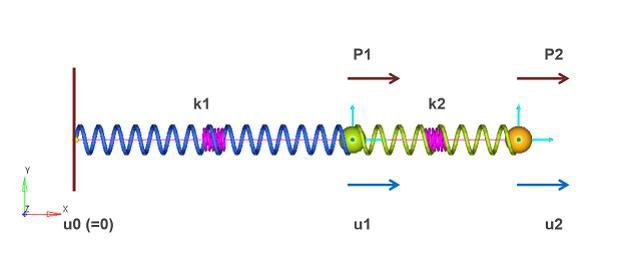
Figure 1. Springs in Series – Model DescriptionA list of properties for the system follows:- Displacement: u0 =0 (Fixed)
- Force:
- P1 = 1N
- P2 = 2N
- Stiffness:
- k1 = 2 N/mm
- k2 = 3 N/mm
- Response Variables (RV): u1 and u2
- Design Variables (DV): k1 and k2
- Analysis Type: Static Analysis with DSA
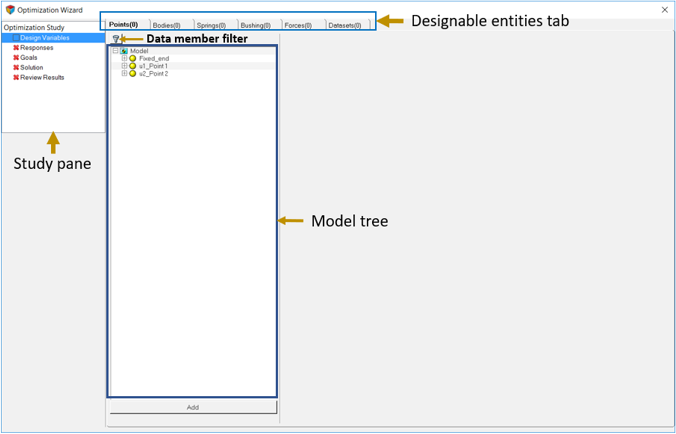
The process of optimization starts with setting up a model in MotionView. MotionView’s Optimization Wizard is used to setup design variables, responses and objectives. The wizard also guides the user to run and plot/print results of optimization. It is also able to export a design from a particular iteration into a new MDL for further analyses.
Add Design Variables
In this step, you will add design variables for the optimization.
Add Response Variables
In this step, you will add response variables for the optimization.
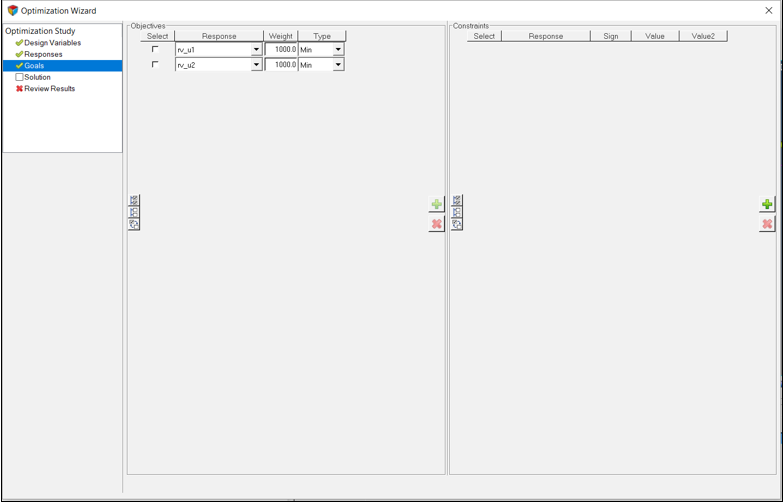
- Displacement u1: To make u1 to reach a value of 3, the metric (1-u1/3)**2 is used.
- Displacement u2: To make u2 to reach a value of 4, the metric (1-u2/4)**2 is used.
Add Objectives and Constraints
Now you will add two objectives to the problem.
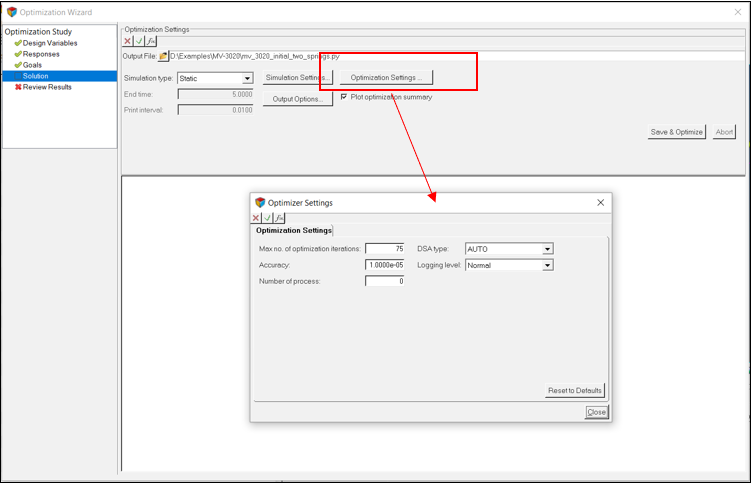
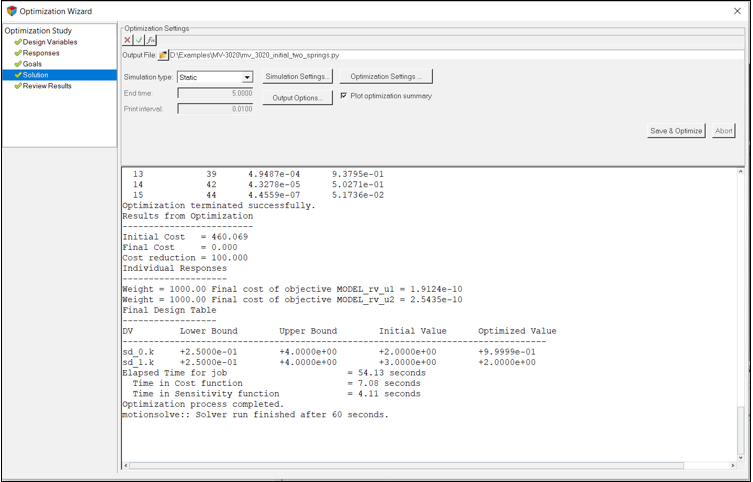
Run the Optimization
In this step you will run the optimization.
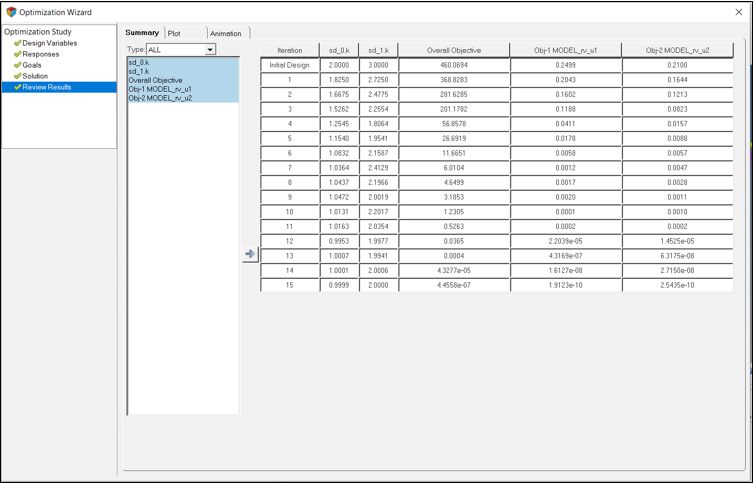
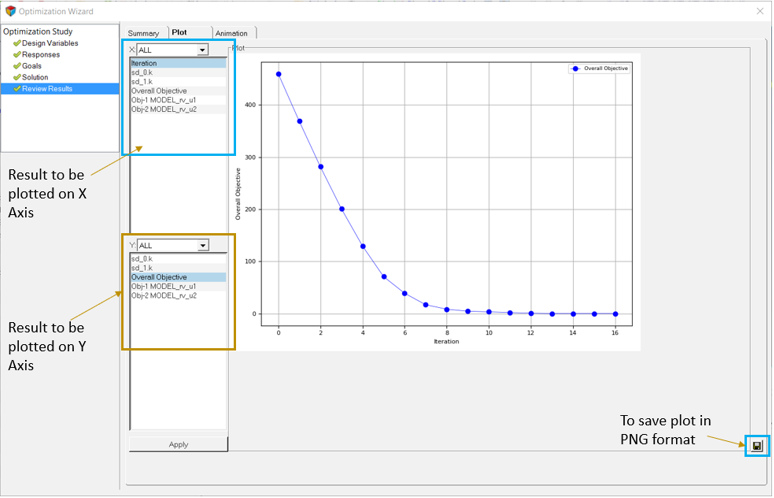
Post-Process
In this step, you will post-process the results of optimization.