SS-V: 4010 Bimetallic Cantilever Beam

Definition

A cantilever beam is built from two equal thickness layers of different metals (Figure 1). The beam is fixed at centerline at one end (translations and rotation around the centerline are set to zero) and is subjected to uniform temperature change of 100 degrees Fahrenheit.

Both layers of materials have the same dimensions 10 x 1 x 0.05 inch.

The material properties are:

Properties

Value

Modulus of Elasticity

3.e+7 psi

Poisson's Ratio

0

Coefficient of thermal expansion: top layer

2.e-5 in/in-F

Coefficient of thermal expansion: bottom layer

1.e-5 in/in-F

Figure 1.

Results

Layers of the beam are simulated by solids glued together. In order to reproduce as close as possible boundary conditions of beam theory used in reference, the edge at centerline at “fixed” end of the beam is constrained in lateral directions. To eliminate rotations around the edge and sliding along the edge a point at the corner of upper fiber is fixed in two directions (Figure 2).

Because the beam is simulated using full 3D solid model, the constraints applied at the beam “fixed” end introduce local disturbances which quickly dissipate along the beam axis (Figure 4).

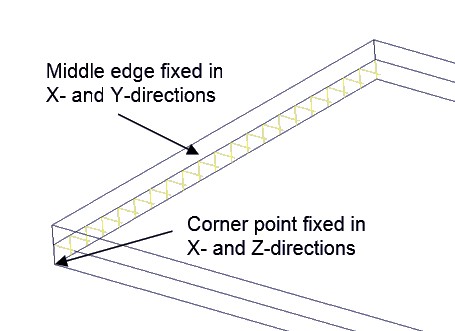
Figure 2. Constraints at ‘fixed” end

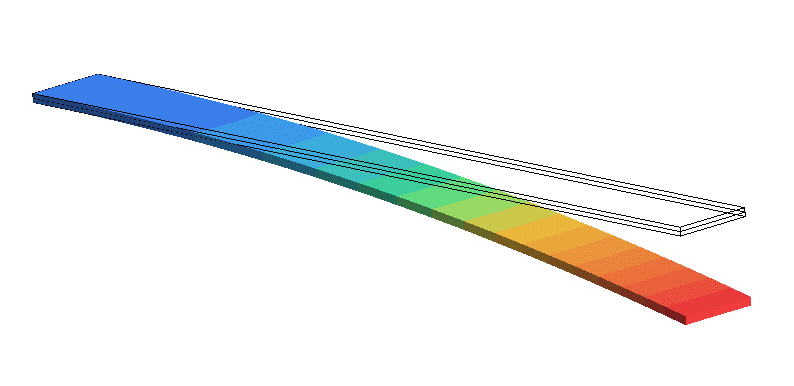
Figure 3. Beam deformation

Figure 4. Distribution of bending stress X at “fixed” end