Far Fields

View the quantities and properties that are available for a far field request.

On the Home tab, in the Add results group, click the  Far Field Source icon.

The options available for far fields:

Total

The total value independent of the polarisation.

Theta

The vertical (or $\theta$ ) component.

Phi

The horizontal (or $\varphi$ ) component.

Ludwig III (Co)

The reference polarisation as defined by Ludwig for conventional measurement configurations. An antenna that is Z directed implied for which the reference polarisation is intended along the $\varphi ={90}^{\circ }$ cut.

(1) $LII{I}_{Co}(\theta ,\varphi )=E(\theta ,\varphi )\cdot \left[\sin \left(\varphi \right){\widehat{i}}_{\theta }+\cos (\varphi ){\widehat{i}}_{\varphi }\right]$

Ludwig III (Cross)

The cross polarisation as defined by Ludwig for conventional measurement configurations. An antenna that is Z directed implied for which the reference polarisation is intended along the $\varphi =0^{\circ }$ .

(2) $LII{I}_{Cross}(\theta ,\varphi )=E(\theta ,\varphi )\cdot \left[\cos \left(\varphi \right){\widehat{i}}_{\theta }-\sin (\varphi ){\widehat{i}}_{\varphi }\right]$

Conventions for the Ludwig coordinate system are defined by the following parameters:

$\theta$ and $\varphi$

Rotational angles in the spherical coordinate system as defined in Feko.

${\stackrel{⌢}{i}}_{\theta }$

Directional unit vector in the $\theta$ direction.

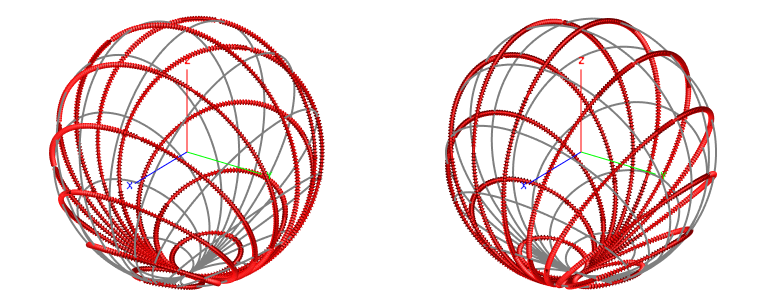
Figure 1. The reference and cross polarisations in 3D space.

LHC

The left hand circularly polarised component. The polarisation vector rotates counter clockwise when viewed from a fixed position in the direction of propagation.

RHC

The left hand circularly polarised component. The polarisation vector rotates counter clockwise when viewed from a fixed position in the direction of propagation.

Z (+45°)

When viewed in the direction of propagation, the $\theta$ unit vector points downwards and the $\varphi ={90}^{\circ }$ unit vector to the left. The Z-polarisation vector is then

(3) ${\widehat{i}}_Z=\frac{\left({\widehat{i}}_{\theta }+{\widehat{i}}_{\varphi }\right)}{\sqrt{2}}$

which lies along an axis rotated +45 degrees from horizontal (in a counter clockwise direction) — coinciding with the direction of the diagonal line of the Z.

S (-45°)

The S-polarisation unit vector is

(4) ${\widehat{i}}_S=\frac{\left({\widehat{i}}_{\theta }+{\widehat{i}}_{\varphi }\right)}{\sqrt{2}}$

which rotated by -45° from horizontal and lies in the direction approximated by the diagonal of the S.

Minor/Major

Displays the magnitude of the axial ratio using the axes specification, Minor/Major.

Major/Minor

Displays the magnitude of the axial ratio using the axes specification, Major/Minor.

Handedness

Displays the sign information for axial ratio on a sphere using different colours for left hand rotating, linear and right rotating fields.