moga
Find constrained minima of a real multi-objective function.
Syntax
x = moga(@func,x0)
x = moga(@func,x0,A,b)
x = moga(@func,x0,A,b,Aeq,beq)
x = moga(@func,x0,A,b,Aeq,beq,lb,ub)
x = moga(@func,x0,A,b,Aeq,beq,lb,ub,nonlcon)
x = moga(@func,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
[x,fval,info,output] = moga(...)
Inputs
- func
- The function to minimize.
- x0
- An estimate of the location of a minimum.
- A
- A matrix used to compute
A*xfor inequality contraints. - b
- The upper bound of the inequality constraints
A*x<=b. - Aeq
- A matrix used to compute
Aeq*xfor equality contraints. - beq
- The upper bound of the equality constraints
Aeq*x=beq. - lb
- The design variable lower bounds.
- ub
- The design variable upper bounds.
- nonlcon
- The non-linear constraints function.
- options
- A struct containing options settings.
Outputs
- x
- The locations of the multi-objective minima.
- fval
- The multi-objective function minima.
- info
- The convergence status flag.
- output
- A struct containing iteration details. The members are as follows.
Examples
function obj = ObjFunc(x)
obj = zeros(2,1);
obj(1) = 2*(x(1)-3)^2 + 4*(x(2)-2)^2 + 6;
obj(2) = 2*(x(1)-3)^2 + 4*(x(2)+2)^2 + 6;
end
init = [2; 0];
lowerBound = [1, -5];
upperBound = [5, 5];
options = mogaoptimset('MaxIter', 40, 'Seed', 2017);
[x,fval,info,output] = moga(@ObjFunc,init,[],[],[],[],lowerBound,upperBound,[],options);
obj1 = output.fvaliter(:,1);
obj2 = output.fvaliter(:,2);
scatter(obj1, obj2);
hold on;
obj1P = fval(:,1);
obj2P = fval(:,2);
scatter(obj1P, obj2P);
legend('Iteration History','Pareto Front');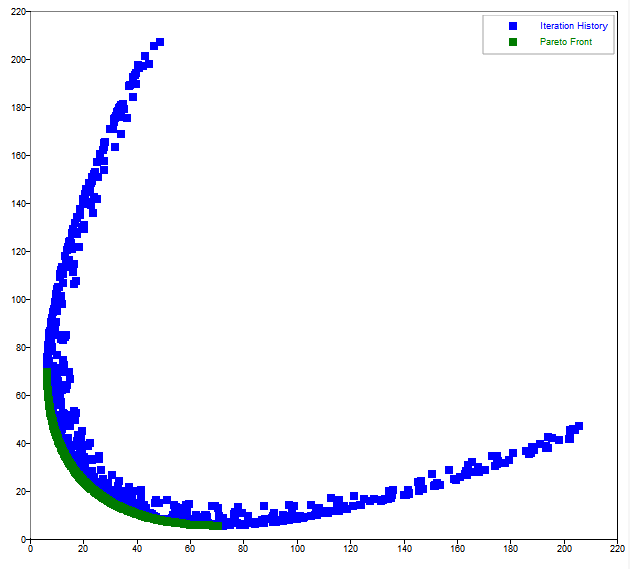
Figure 1. moga figure 1
function obj = ObjFunc(x,p1,p2)
obj = zeros(2,1);
obj(1) = 2*(x(1)-3)^2 + 4*(x(2)-2)^2 + p1;
obj(2) = 2*(x(1)-3)^2 + 4*(x(2)+2)^2 + p2;
end
handle = @(x) ObjFunc(x,7,8);
[x,fval] = moga(handle,init,[],[],[],[],lowerBound,upperBound,[],options);Comments
moga uses a Multi-Objective Genetic Algorithm.
See the fmincon optimization tutorial for an example with nonlinear constraints.
- MaxIter: 50
- MaxFail: 20000
- PopulationSize: 0 (the algorithm chooses)
- TolCon: 0.5 (%)
- CrowdDist: 0
- Seed: 0
- Display: 'off'
Unbounded limits design variable limits are not fully supported and are set to -1000 and 1000. Use of large limits is discouraged due to the size of the search area.
To pass additional parameters to a function argument, use an anonymous function.