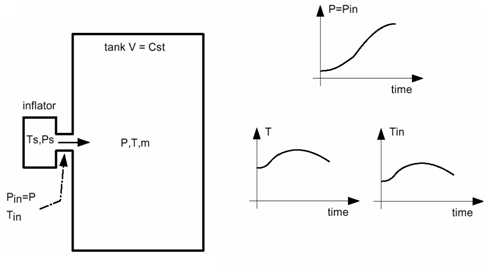
By using data from a tank test output, it is possible to obtain the temperature and
the mass flow of the gas supplied, which can be used as input to Radioss .
With a tank test it is possible to measure the pressure at the injection point or in
the middle of the tank, the two values are equal so the pressure variation is well
known. Also, the amount of gas supplied and the characteristics of the gas in the
test are known.
For temperature, it is more difficult to get accurate test data because the
temperature gauges are often not accurate enough. Therefore, the temperature from
the tank test may be wrong.
Figure 1. Unknown Mass Flow Rate
The following cases take into account that you may or may not know the injected
temperature and the temperature in the tank.
In case the temperature at the injector and in the tank is not known:
Initial and injected gas composition Knowing the molecular weight (
M
W
i
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGnbGaam
4vamaaBaaaleaacaWGPbaabeaaaaa@3927@
) of each elements and the molar fraction (
X
i
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGybWaaS
baaSqaaiaadMgaaeqaaaaa@3856@
), it is possible to define the molar
weight of the gas (
M
W
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGnbGaam
4vaaaa@380D@
):
(1)
M W =
∑
X
i
⋅ M
W
i
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGnbGaam
4vaiabg2da9maaqaeabaGaamiwamaaBaaaleaacaWGPbaabeaakiab
gwSixlaad2eacaWGxbWaaSbaaSqaaiaadMgaaeqaaaqabeqaniabgg
HiLdaaaa@422F@
The average heat capacity, per mass unit of a mixture of gases is given by the Amagat-Leduc
equation:
(2)
C
p
(
T
) =
∑
m
i
⋅
C
p a
∑
m
i
+
∑
m
i
⋅
C
p b
∑
m
i
T +
∑
m
i
⋅
C
p c
∑
m
i
T
2
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGdbWaaS
baaSqaaiaadchaaeqaaOWaaeWaaeaacaWGubaacaGLOaGaayzkaaGa
eyypa0ZaaSaaaeaadaaeabqaaiaad2gadaWgaaWcbaGaamyAaaqaba
GccqGHflY1caWGdbWaaSbaaSqaaiaadchacaWGHbaabeaaaeqabeqd
cqGHris5aaGcbaWaaabqaeaacaWGTbWaaSbaaSqaaiaadMgaaeqaaa
qabeqaniabggHiLdaaaOGaey4kaSYaaSaaaeaadaaeabqaaiaad2ga
daWgaaWcbaGaamyAaaqabaGccqGHflY1caWGdbWaaSbaaSqaaiaadc
hacaWGIbaabeaaaeqabeqdcqGHris5aaGcbaWaaabqaeaacaWGTbWa
aSbaaSqaaiaadMgaaeqaaaqabeqaniabggHiLdaaaOGaamivaiabgU
caRmaalaaabaWaaabqaeaacaWGTbWaaSbaaSqaaiaadMgaaeqaaOGa
eyyXICTaam4qamaaBaaaleaacaWGWbGaam4yaaqabaaabeqab0Gaey
yeIuoaaOqaamaaqaeabaGaamyBamaaBaaaleaacaWGPbaabeaaaeqa
beqdcqGHris5aaaakiaadsfadaahaaWcbeqaaiaaikdaaaaaaa@686E@
Using the previous equation, the heat capacity coefficients (
C
p
(
T
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4qamaaBa
aaleaacaWGWbaabeaakiaacIcacaWGubGaaiykaaaa@3A1B@
) of the initial and injected mixture may be
defined.
Knowing the characteristics of the injected gas, the initial gas, and the mixture, it
is possible to find the mass flow and the temperature for the inflator. The
following basic equations are used to carry out the analysis.
The perfect gas equation of state is:(3)
P
V
=
n
R
T
,
n
=
m
M
W
R
=
8.314
J
m
o
l
e
⋅
K
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGsbGaey
ypa0JaaGioaiaac6cacaaIZaGaaGymaiaaisdadaWcaaqaaiaacQea
aeaacaGGTbGaai4BaiaacYgacaGGLbGaeyyXICTaai4saaaaaaa@4399@
And the adiabatic equation:(4)
H
=
c
o
n
s
t
.
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGibGaey
ypa0Jaam4yaiaad+gacaWGUbGaam4CaiaadshacaGGUaaaaa@3DA3@
H
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGibaaaa@372B@
being the total enthalpy of the system
(inflator + tank).
From the conservation of the energy, the basic energy equation of the tank test can
be written as:
(5)
d
E
a i r b a g
= − P d V + d
H
i n
− d
H
o u t
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGKbGaam
yramaaBaaaleaacaWGHbGaamyAaiaadkhacaWGIbGaamyyaiaadEga
aeqaaOGaeyypa0JaeyOeI0IaamiuaiaadsgacaWGwbGaey4kaSIaam
izaiaadIeadaWgaaWcbaGaamyAaiaad6gaaeqaaOGaeyOeI0Iaamiz
aiaadIeadaWgaaWcbaGaam4BaiaadwhacaWG0baabeaaaaa@4CBC@
Here
d
H
o
u
t
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGKbGaam
isamaaBaaaleaacaWGVbGaamyDaiaadshaaeqaaaaa@3B27@
=0, since the tank test is adiabatic. The constant
volume of the tank test means
d
V
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGKbGaam
Ovaaaa@3822@
=0.
Therefore,
Equation 5 is summarized
as:
(6)
U
f
−
U
0
=
d
H
i
n
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGvbWaaS
baaSqaaiaadAgaaeqaaOGaeyOeI0IaamyvamaaBaaaleaacaaIWaaa
beaakiabg2da9iaadsgacaWGibWaaSbaaSqaaiaadMgacaWGUbaabe
aaaaa@3FD9@
⇔
∫
0
T
m i x
m
(
i n + a i r
)
⋅
C
V (
i n + a i r
)
d T −
∫
0
T
a i r
m
(
a i r
)
⋅
C
V (
a i r
)
d T =
∫
0
T
i n
m
(
i n
)
⋅
C
P (
i n
)
d T
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacqGHuhY2da
WdXbqaaiaad2gadaWgaaWcbaWaaeWaaeaacaWGPbGaamOBaiabgUca
RiaadggacaWGPbGaamOCaaGaayjkaiaawMcaaaqabaaabaGaaGimaa
qaaiaadsfadaWgaaadbaGaamyBaiaadMgacaWG4baabeaaa0Gaey4k
IipakiabgwSixlaadoeadaWgaaWcbaGaamOvamaabmaabaGaamyAai
aad6gacqGHRaWkcaWGHbGaamyAaiaadkhaaiaawIcacaGLPaaaaeqa
aOGaamizaiaadsfacqGHsisldaWdXbqaaiaad2gadaWgaaWcbaWaae
WaaeaacaWGHbGaamyAaiaadkhaaiaawIcacaGLPaaaaeqaaaqaaiaa
icdaaeaacaWGubWaaSbaaWqaaiaadggacaWGPbGaamOCaaqabaaani
abgUIiYdGccqGHflY1caWGdbWaaSbaaSqaaiaadAfadaqadaqaaiaa
dggacaWGPbGaamOCaaGaayjkaiaawMcaaaqabaGccaWGKbGaamivai
abg2da9maapehabaGaamyBamaaBaaaleaadaqadaqaaiaadMgacaWG
UbaacaGLOaGaayzkaaaabeaaaeaacaaIWaaabaGaamivamaaBaaame
aacaWGPbGaamOBaaqabaaaniabgUIiYdGccqGHflY1caWGdbWaaSba
aSqaaiaadcfadaqadaqaaiaadMgacaWGUbaacaGLOaGaayzkaaaabe
aakiaadsgacaWGubaaaa@815B@
⇔
m
(
m i x
)
T
m i x
(
C
p a (
m i x
)
+
C
p b (
m i x
)
T
m i x
2
+
C
p c (
m i x
)
T
m i x
2
3
−
R
M
W
m i x
) −
m
(
a i r
)
T
0
(
C
p a (
a i r
)
+
C
p b (
a i r
)
T
0
2
+
C
p c (
a i r
)
T
0
2
3
−
R
M
W
a i r
) =
m
(
i n
)
T
i n
(
C
p a (
i n
)
+
C
p b (
i n
)
T
i n
2
+
C
p c (
i n
)
T
i n
2
3
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakqaabeqaaiabgs
DiBlaad2gadaWgaaWcbaWaaeWaaeaacaWGTbGaamyAaiaadIhaaiaa
wIcacaGLPaaaaeqaaOGaamivamaaBaaaleaacaWGTbGaamyAaiaadI
haaeqaaOWaaeWaaeaacaWGdbWaaSbaaSqaaiaadchacaWGHbWaaeWa
aeaacaWGTbGaamyAaiaadIhaaiaawIcacaGLPaaaaeqaaOGaey4kaS
Iaam4qamaaBaaaleaacaWGWbGaamOyamaabmaabaGaamyBaiaadMga
caWG4baacaGLOaGaayzkaaaabeaakmaalaaabaGaamivamaaBaaale
aacaWGTbGaamyAaiaadIhaaeqaaaGcbaGaaGOmaaaacqGHRaWkcaWG
dbWaaSbaaSqaaiaadchacaWGJbWaaeWaaeaacaWGTbGaamyAaiaadI
haaiaawIcacaGLPaaaaeqaaOWaaSaaaeaacaWGubWaaSbaaSqaaiaa
d2gacaWGPbGaamiEaaqabaGcdaahaaWcbeqaaiaaikdaaaaakeaaca
aIZaaaaiabgkHiTmaalaaabaGaamOuaaqaaiaad2eacaWGxbWaaSba
aSqaaiaad2gacaWGPbGaamiEaaqabaaaaaGccaGLOaGaayzkaaGaey
OeI0IaamyBamaaBaaaleaadaqadaqaaiaadggacaWGPbGaamOCaaGa
ayjkaiaawMcaaaqabaGccaWGubWaaSbaaSqaaiaaicdaaeqaaaGcba
WaaeWaaeaacaWGdbWaaSbaaSqaaiaadchacaWGHbWaaeWaaeaacaWG
HbGaamyAaiaadkhaaiaawIcacaGLPaaaaeqaaOGaey4kaSIaam4qam
aaBaaaleaacaWGWbGaamOyamaabmaabaGaamyyaiaadMgacaWGYbaa
caGLOaGaayzkaaaabeaakmaalaaabaGaamivamaaBaaaleaacaaIWa
aabeaaaOqaaiaaikdaaaGaey4kaSIaam4qamaaBaaaleaacaWGWbGa
am4yamaabmaabaGaamyyaiaadMgacaWGYbaacaGLOaGaayzkaaaabe
aakmaalaaabaGaamivamaaBaaaleaacaaIWaaabeaakmaaCaaaleqa
baGaaGOmaaaaaOqaaiaaiodaaaGaeyOeI0YaaSaaaeaacaWGsbaaba
GaamytaiaadEfadaWgaaWcbaGaamyyaiaadMgacaWGYbaabeaaaaaa
kiaawIcacaGLPaaacqGH9aqpcaWGTbWaaSbaaSqaamaabmaabaGaam
yAaiaad6gaaiaawIcacaGLPaaaaeqaaOGaamivamaaBaaaleaacaWG
PbGaamOBaaqabaGcdaqadaqaaiaadoeadaWgaaWcbaGaamiCaiaadg
gadaqadaqaaiaadMgacaWGUbaacaGLOaGaayzkaaaabeaakiabgUca
RiaadoeadaWgaaWcbaGaamiCaiaadkgadaqadaqaaiaadMgacaWGUb
aacaGLOaGaayzkaaaabeaakmaalaaabaGaamivamaaBaaaleaacaWG
PbGaamOBaaqabaaakeaacaaIYaaaaiabgUcaRiaadoeadaWgaaWcba
GaamiCaiaadogadaqadaqaaiaadMgacaWGUbaacaGLOaGaayzkaaaa
beaakmaalaaabaGaamivamaaBaaaleaacaWGPbGaamOBaaqabaGcda
ahaaWcbeqaaiaaikdaaaaakeaacaaIZaaaaaGaayjkaiaawMcaaaaa
aa@C0F8@
Inflator Temperature
In Equation 6 , the unknown variable is only
T
i
n
i
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamivamaaBa
aaleaacaWGPbGaamOBaiaadMgaaeqaaaaa@39CA@
.
The other variables are known or could be determined using
Equation 2 and
Equation 3 :
m
(
i
n
)
m
(
a
i
r
)
=
M
W
a
i
r
P
0
V
R
T
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGTbWaaS
baaSqaamaabmaabaGaamyAaiaad6gaaiaawIcacaGLPaaaaeqaaOGa
amyBamaaBaaaleaadaqadaqaaiaadggacaWGPbGaamOCaaGaayjkai
aawMcaaaqabaGccqGH9aqpcaWGnbGaam4vamaaBaaaleaacaWGHbGa
amyAaiaadkhaaeqaaOWaaSaaaeaacaWGqbWaaSbaaSqaaiaaicdaae
qaaOGaamOvaaqaaiaadkfacaWGubWaaSbaaSqaaiaaicdaaeqaaaaa
aaa@4B67@
and
n
(
m
i
x
)
=
m
(
i
n
)
M
W
i
n
+
m
(
a
i
r
)
M
W
a
i
r
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGUbWaaS
baaSqaamaabmaabaGaamyBaiaadMgacaWG4baacaGLOaGaayzkaaaa
beaakiabg2da9maalaaabaGaamyBamaaBaaaleaadaqadaqaaiaadM
gacaWGUbaacaGLOaGaayzkaaaabeaaaOqaaiaad2eacaWGxbWaaSba
aSqaaiaadMgacaWGUbaabeaaaaGccqGHRaWkdaWcaaqaaiaad2gada
WgaaWcbaWaaeWaaeaacaWGHbGaamyAaiaadkhaaiaawIcacaGLPaaa
aeqaaaGcbaGaamytaiaadEfadaWgaaWcbaGaamyyaiaadMgacaWGYb
aabeaaaaaaaa@506D@
for i =
a to
c :
C
p
i
(
i
n
)
,
C
p
i
(
a
i
r
)
,
C
p
i
(
m
i
x
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGdbWaaS
baaSqaaiaadchacaWGPbaabeaakmaaBaaaleaadaqadaqaaiaadMga
caWGUbaacaGLOaGaayzkaaaabeaakiaacYcacaWGdbWaaSbaaSqaai
aadchacaWGPbaabeaakmaaBaaaleaadaqadaqaaiaadggacaWGPbGa
amOCaaGaayjkaiaawMcaaaqabaGccaGGSaGaam4qamaaBaaaleaaca
WGWbGaamyAaaqabaGcdaWgaaWcbaWaaeWaaeaacaWGTbGaamyAaiaa
dIhaaiaawIcacaGLPaaaaeqaaaaa@4D1D@
are calculated with Equation 2 , and
T
m
i
x
=
P
t
a
n
k
V
t
a
n
k
n
(
m
i
x
)
R
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGubWaaS
baaSqaaiaad2gacaWGPbGaamiEaaqabaGccqGH9aqpdaWcaaqaaiaa
dcfadaWgaaWcbaGaamiDaiaadggacaWGUbGaam4AaaqabaGccaWGwb
WaaSbaaSqaaiaadshacaWGHbGaamOBaiaadUgaaeqaaaGcbaGaamOB
amaaBaaaleaacaGGOaGaamyBaiaadMgacaWG4bGaaiykaaqabaGcca
WGsbaaaaaa@4B36@
Therefore, Equation 6 finds the
temperature at the injector
T
i
n
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamivamaaBa
aaleaacaWGPbGaamOBaiaadMgaaeqaaaaa@39CA@
of the injected gas by iterating on
T
i
n
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamivamaaBa
aaleaacaWGPbGaamOBaiaadMgaaeqaaaaa@39CA@
. First, the temperature is guessed and six
iterations are sufficient to converge to the solution.
Mass Flow
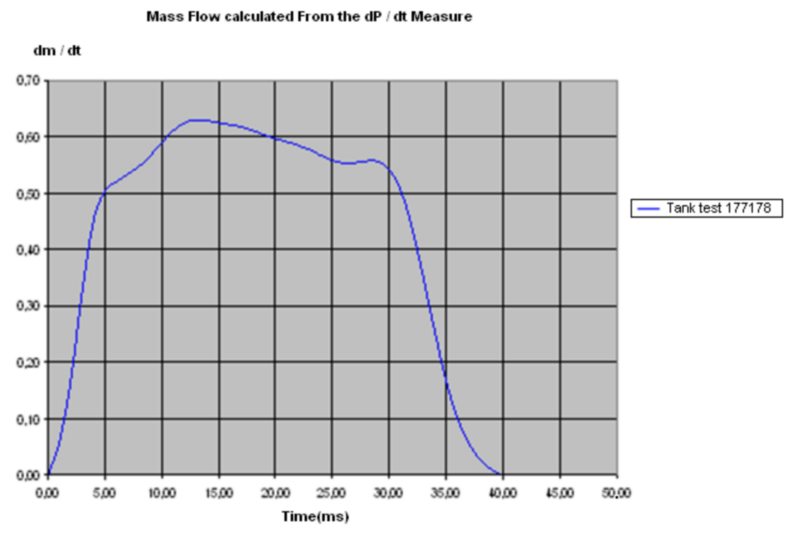
Knowing the evolution of the pressure versus time at the top of the tank test, it is possible to
determine the mass flow rate with:
(7)
m
˙
=
∂ m
∂ P
∂ P
∂ t
≅
Δ M
Δ P
∂ P
∂ t
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaceWGTbGbai
aacqGH9aqpdaWcaaqaaiabgkGi2kaad2gaaeaacqGHciITcaWGqbaa
amaalaaabaGaeyOaIyRaamiuaaqaaiabgkGi2kaadshaaaGaeyyrIa
0aaSaaaeaacqqHuoarcaWGnbaabaGaeuiLdqKaamiuaaaadaWcaaqa
aiabgkGi2kaadcfaaeaacqGHciITcaWG0baaaaaa@4C0C@
With,
Δ
P
Total pressure variation during the experiment
Δ
M
Total injected mass
Equation 7 may be written
if the variation of mass versus the variation of the pressure is a function strictly
growing, which is the case.
Figure 2. Mass Flow Curve - Evolution of the Mass Flow versus Time
Inflator Gas Velocity
Since the pressure is quickly uniform, the following equation may be written:
P
i
n
=
P
(
t
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGqbWaaS
baaSqaaiaadMgacaWGUbaabeaakiabg2da9iaadcfacaGGOaGaamiD
aiaacMcaaaa@3D77@
, knowing
T
i
n
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamivamaaBa
aaleaacaWGPbGaamOBaiaadMgaaeqaaaaa@39CA@
the density may be expressed as a function of
T
i
n
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamivamaaBa
aaleaacaWGPbGaamOBaiaadMgaaeqaaaaa@39CA@
and
P
(
t
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGqbGaai
ikaiaadshacaGGPaaaaa@3985@
:
(8)
ρ
i n
=
P ( t )
T
i n
R
M
W
i n
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacqaHbpGCda
WgaaWcbaGaamyAaiaad6gaaeqaaOGaeyypa0ZaaSaaaeaacaWGqbGa
aiikaiaadshacaGGPaaabaWaaSGaaeaacaWGubWaaSbaaSqaaiaadM
gacaWGUbaabeaakiaadkfaaeaacaWGnbGaam4vamaaBaaaleaacaWG
PbGaamOBaaqabaaaaaaaaaa@4606@
Besides,
V
i
n
(
t
)
=
d
m
(
t
)
d
t
S
ρ
i
n
(
t
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGwbWaaS
baaSqaaiaadMgacaWGUbaabeaakiaacIcacaWG0bGaaiykaiabg2da
9maalaaabaWaaSGaaeaacaWGKbGaamyBaiaacIcacaWG0bGaaiykaa
qaaiaadsgacaWG0baaaaqaaiaadofacqaHbpGCdaWgaaWcbaGaamyA
aiaad6gaaeqaaOGaaiikaiaadshacaGGPaaaaaaa@49DA@
, the sound speed into the gas is equal
to:
(9)
c
i
n
2
=
γ
R
M
W
i
n
T
i
n
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGJbWaaS
baaSqaaiaadMgacaWGUbaabeaakmaaCaaaleqabaGaaGOmaaaakiab
g2da9iabeo7aNnaalaaabaGaamOuaaqaaiaad2eacaWGxbWaaSbaaS
qaaiaadMgacaWGUbaabeaaaaGccaWGubWaaSbaaSqaaiaadMgacaWG
Ubaabeaaaaa@448F@
and if
V
i
n
>
c
i
n
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGwbWaaS
baaSqaaiaadMgacaWGUbaabeaakiabg6da+iaadogadaWgaaWcbaGa
amyAaiaad6gaaeqaaaaa@3D4D@
, then
V
i
n
=
c
i
n
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGwbWaaS
baaSqaaiaadMgacaWGUbaabeaakiabg2da9iaadogadaWgaaWcbaGa
amyAaiaad6gaaeqaaaaa@3D4B@
the velocity is major by the sound speed
velocity.
If the injector temperature is known:
d
m
d
t
=
v
γ
(
γ
−
1
)
C
V
T
i
n
d
P
d
t
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWcaaqaai
aadsgacaWGTbaabaGaamizaiaadshaaaGaeyypa0ZaaSaaaeaacaWG
2baabaGaeq4SdC2aaeWaaeaacqaHZoWzcqGHsislcaaIXaaacaGLOa
GaayzkaaGaam4qamaaBaaaleaacaWGwbaabeaakiaadsfadaWgaaWc
baGaamyAaiaad6gaaeqaaaaakmaalaaabaGaamizaiaadcfaaeaaca
WGKbGaamiDaaaaaaa@4B34@
If the temperature in the tank is known:
d
m
d
t
=
V
γ
(
γ
−
1
)
C
V
T
2
(
T
d
P
d
t
−
P
d
T
d
t
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWcaaqaai
aadsgacaWGTbaabaGaamizaiaadshaaaGaeyypa0ZaaSaaaeaacaWG
wbaabaGaeq4SdC2aaeWaaeaacqaHZoWzcqGHsislcaaIXaaacaGLOa
GaayzkaaGaam4qamaaBaaaleaacaWGwbaabeaakiaadsfadaahaaWc
beqaaiaaikdaaaaaaOWaaeWaaeaacaWGubWaaSaaaeaacaWGKbGaam
iuaaqaaiaadsgacaWG0baaaiabgkHiTiaadcfadaWcaaqaaiaadsga
caWGubaabaGaamizaiaadshaaaaacaGLOaGaayzkaaaaaa@51C8@
or
m
=
P
V
(
γ
−
1
)
C
V
T
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGTbGaey
ypa0ZaaSaaaeaacaWGqbGaamOvaaqaamaabmaabaGaeq4SdCMaeyOe
I0IaaGymaaGaayjkaiaawMcaaiaadoeadaWgaaWcbaGaamOvaaqaba
GccaWGubaaaaaa@41A0@
T
i
n
=
T
2
γ
(
d
P
d
t
T
d
P
d
t
−
P
d
T
d
t
)
or
T
i
n
=
T
γ
+
m
γ
d
T
d
t
d
m
d
t
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGubWaaS
baaSqaaiaadMgacaWGUbaabeaakiabg2da9maalaaabaGaamivamaa
CaaaleqabaGaaGOmaaaaaOqaaiabeo7aNbaadaqadaqaamaalaaaba
WaaSaaaeaacaWGKbGaamiuaaqaaiaadsgacaWG0baaaaqaaiaadsfa
daWcaaqaaiaadsgacaWGqbaabaGaamizaiaadshaaaGaeyOeI0Iaam
iuamaalaaabaGaamizaiaadsfaaeaacaWGKbGaamiDaaaaaaaacaGL
OaGaayzkaaGaaGzbVlaab+gacaqGYbGaaGzbVlaadsfadaWgaaWcba
GaamyAaiaad6gaaeqaaOGaeyypa0ZaaSaaaeaacaWGubaabaGaeq4S
dCgaaiabgUcaRmaalaaabaGaamyBaaqaaiabeo7aNbaadaWcaaqaam
aalaaabaGaamizaiaadsfaaeaacaWGKbGaamiDaaaaaeaadaWcaaqa
aiaadsgacaWGTbaabaGaamizaiaadshaaaaaaaaa@63C4@
If the temperature in the tank is constant:
T
i
n
=
T
γ
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGubWaaS
baaSqaaiaadMgacaWGUbaabeaakiabg2da9maalaaabaGaamivaaqa
aiabeo7aNbaaaaa@3CE4@