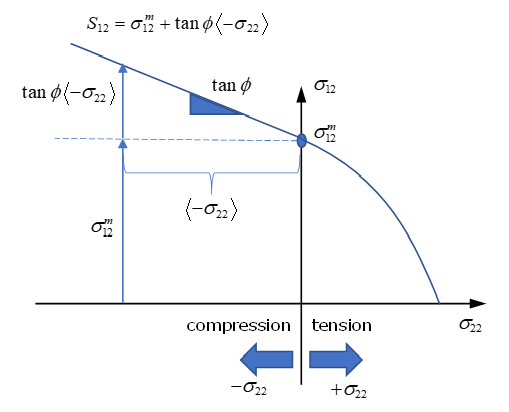
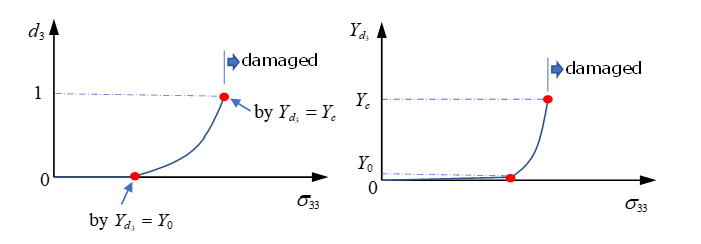
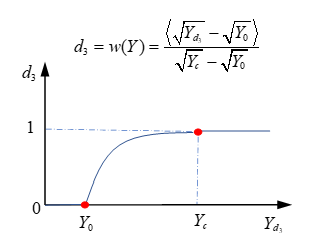
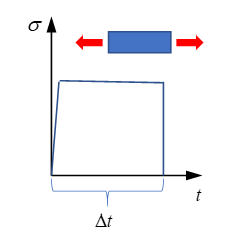
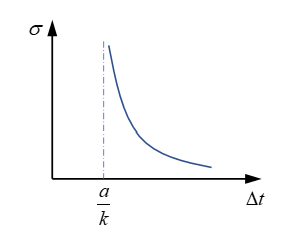
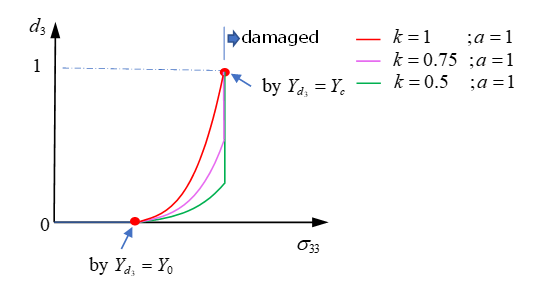
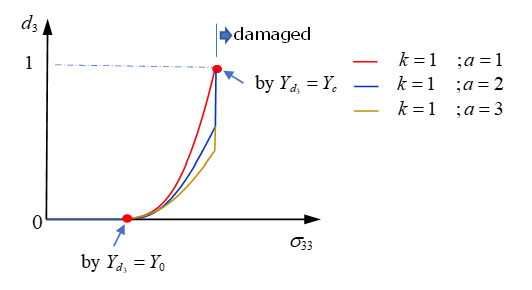
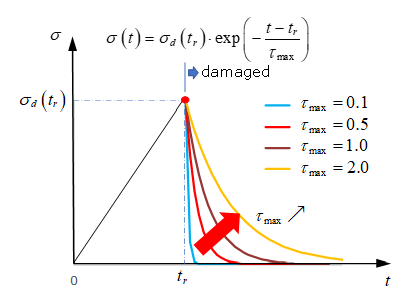
| Damage criteria |
If =1, then failure. If , then no failure.
With
|
If =1, then failure. If , then no failure.
With
|
| Tensile/shear fiber mode |
|
With,
|
| Compression fiber mode |
With
|
With
With
|
| Crush mode |
With
|
With
|
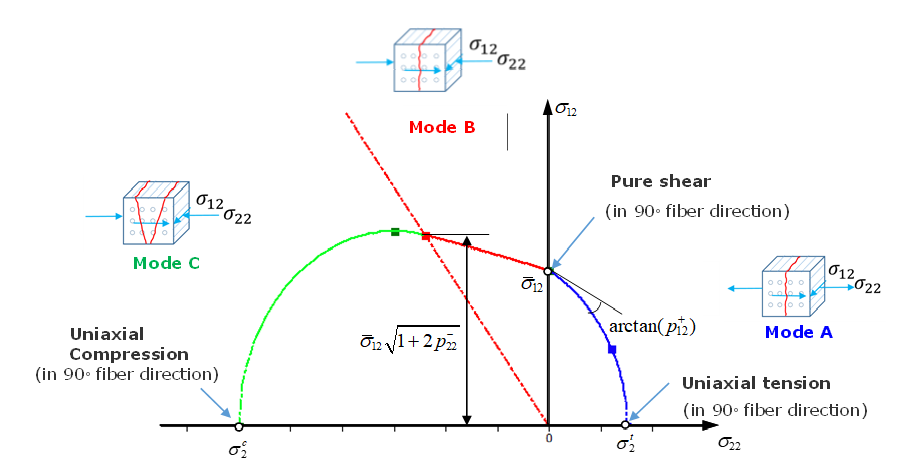
| Shear failure matrix mode |
|
|
| Failure matrix mode |
Where,
|
|
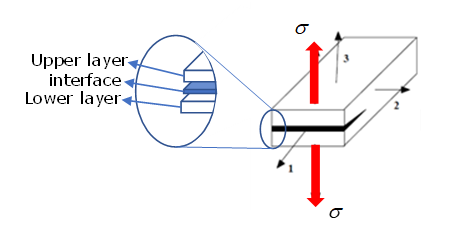
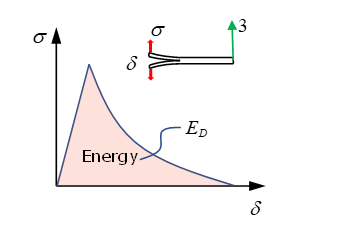
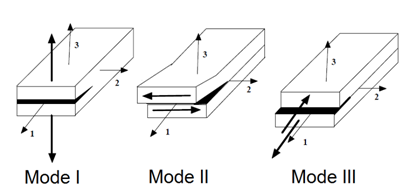
| Delamination mode |
Where,
|
Where,
|